题目内容
（2011•渭南三模）定义域为R的偶函数f（x），当x＞0时，f(x)=
，若方程f2（x）+bf（x）+c=0有5个不同的实根，则5根之和为
| 1 | x |
0
0
．分析：先根据一元二次方程根的情况可判断f（x）=常数a，一定是三个解，再根据f（x）的图象可知f（x）=a有三解时，根据图象的对称性可知所求5根之和．
解答：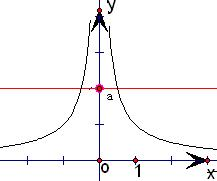
解：定义域为R的偶函数f（x），当x＞0时，f(x)=
，
根据偶函数的对称性，作出其图象如图所示，
设关于x的方程f2（x）+bf（x）+c=0有且只有5个不同的实数根x1，x2，x3，x4，x5，且x1＜x2＜x3＜x4＜x5，
又f（x）=常数a，x最多三解．
而题目要求f2（x）+bf（x）+c=0有5解，即可推断f（x）=a为三解！
算出x3=0，x2+x4=0，x1+x5=0；
所以：x1+x2+x3+x4+x5=0；
故答案为：0．
解：定义域为R的偶函数f（x），当x＞0时，f(x)=| 1 |
| x |
根据偶函数的对称性，作出其图象如图所示，
设关于x的方程f2（x）+bf（x）+c=0有且只有5个不同的实数根x1，x2，x3，x4，x5，且x1＜x2＜x3＜x4＜x5，
又f（x）=常数a，x最多三解．
而题目要求f2（x）+bf（x）+c=0有5解，即可推断f（x）=a为三解！
算出x3=0，x2+x4=0，x1+x5=0；
所以：x1+x2+x3+x4+x5=0；
故答案为：0．
点评：本题主要考查根的存在性及根的个数判断、偶函数图象的对称性，考查基础知识的综合运用能力，以及数形结合的思想，属于中档题．
练习册系列答案
相关题目
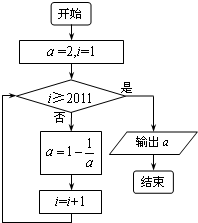（2011•渭南三模）已知某程序框图如图所示，则执行该程序后输出的结果是（ ）
（2011•渭南三模）已知正三棱柱的侧面积为36，其三视图如图所示，则它的左视图的面积为（ ）