题目内容
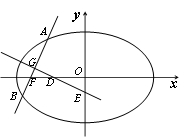
(附加题)如图,椭圆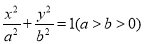 的左焦点为
的左焦点为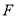 ,过点
,过点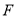 的直线交椭圆于
的直线交椭圆于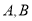 两点.
两点.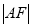 的最大值是
的最大值是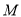 ,
,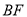 的最小值是
的最小值是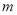 ,满足
,满足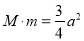 .
.
(1)求该椭圆的离心率;
(2)设线段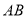 的中点为
的中点为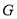 ,
,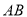 的垂直平分线与
的垂直平分线与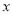 轴和
轴和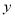 轴分别交于
轴分别交于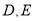 两点,
两点,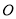 是坐标原点.记
是坐标原点.记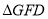 的面积为
的面积为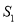 ,
,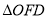 的面积为
的面积为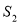 ,求
,求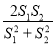 的取值范围.
的取值范围.
(1)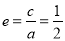 ;(2)
;(2)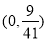 .
.
【解析】
试题分析:(1)根据椭圆性质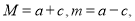 进行求解;(2)设出直线方程
进行求解;(2)设出直线方程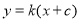 ,联立直线与椭圆方程,利用“设而不求”的方法以及中点坐标公式求得
,联立直线与椭圆方程,利用“设而不求”的方法以及中点坐标公式求得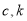 的关系,再利用垂直与三角形的相似行求解.
的关系,再利用垂直与三角形的相似行求解.
解题思路:1.处理直线与椭圆的位置关系时,往往采用“设而不求”的方法进行求解;
2.在处理解析几何问题时,灵活恰当地利用平面几何知识可使运算简化.
试题解析:(1)设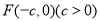 ,则根据椭圆性质得
,则根据椭圆性质得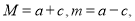 而
而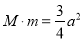 ,
,
所以有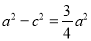 ,即
,即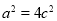 ,
,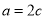 ,因此椭圆的离心率为
,因此椭圆的离心率为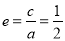 .
.
(2)由(1)可知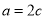 ,
, 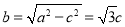 ,椭圆的方程为
,椭圆的方程为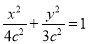 .
.
根据条件直线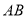 的斜率一定存在且不为零,设直线
的斜率一定存在且不为零,设直线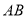 的方程为
的方程为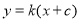 ,
,
并设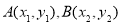 则由
则由 消去
消去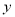 并整理得
并整理得
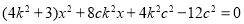
从而有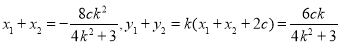 ,
,
所以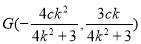 .
.
因为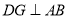 ,所以
,所以 ,
,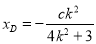 .
.
由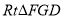 与
与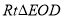 相似,所以
相似,所以
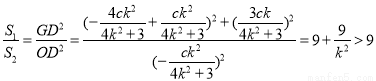 .
.
令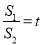 ,则
,则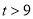 ,从而
,从而
 ,即
,即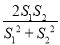 的取值范围是
的取值范围是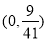 .
.
考点:1.椭圆的标准方程;2.直线与椭圆的位置关系.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
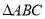 的内角
的内角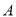 ,
,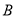 ,
,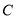 所对的边长分别为
所对的边长分别为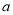 ,
,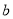 ,
,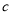 且
且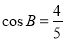 ,
, .
. ,求
,求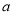 的值;
的值;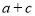 的值
的值 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )  C.
C. D.
D.
 ,设
,设 ,
,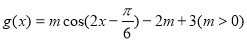 ,若对任意
,若对任意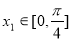 都存在
都存在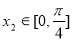 ,使得
,使得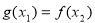 成立。则实数
成立。则实数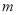 的取值范围是
的取值范围是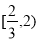 B.
B.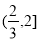 C.
C.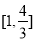 D.
D.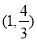
 是第三象限角,且
是第三象限角,且 ,则
,则
 B.
B. C.
C. D.
D.
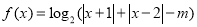 .
.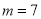 时,求函数
时,求函数 的定义域;
的定义域;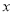 的不等式
的不等式 的解集是
的解集是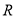 ,求
,求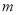 的取值范围.
的取值范围. 满足
满足 时,则
时,则 的最大值是( )
的最大值是( ) ,M是
,M是 上的动点,则|MN|的最小值是 。
上的动点,则|MN|的最小值是 。 ;
;  .
.