题目内容
若△ABC满足
=3cos(A+B),则tanB的最大值是
.
| sinB |
| sinA |
| 3 |
| 4 |
| 3 |
| 4 |
分析:由A和B为三角形的内角,得到sinA和sinB都大于0,进而确定出C为钝角,利用诱导公式及三角形的内角和定理化简已知等式的左边,得到sinB=-3sinAcosC,再由sinB=sin(A+C),利用两角和与差的正弦函数公式化简,再利用同角三角函数间的基本关系化简,得到tanC=-4tanA,将tanB利用诱导公式及三角形的内角和定理化简为-tan(A+C),利用两角和与差的正切函数公式化简,将tanC=-4tanA代入,变形后利用基本不等式求出tanB的范围,即可得到tanB的最大值.
解答:解:∵sinA>0,sinB>0,
∴
=3cos(A+B)=-3cosC>0,即cosC<0,
∴C为钝角,sinB=-3sinAcosC,
又sinB=sin(A+C)=sinAcosC+cosAsinC,
∴sinAcosC+cosAsinC=-3sinAcosC,即cosAsinC=-4sinAcosC,
∴tanC=-4tanA,
∴tanB=-tan(A+C)=-
=-
=
≤
,
当且仅当
=4tanA,即tanA=
时取等号,
则tanB的最大值为
.
故答案为:
.
∴
| sinB |
| sinA |
∴C为钝角,sinB=-3sinAcosC,
又sinB=sin(A+C)=sinAcosC+cosAsinC,
∴sinAcosC+cosAsinC=-3sinAcosC,即cosAsinC=-4sinAcosC,
∴tanC=-4tanA,
∴tanB=-tan(A+C)=-
| tanA+tanC |
| 1-tanAtanC |
| -3tanA |
| 1+4tan2A |
| 3 | ||
|
| 3 |
| 4 |
当且仅当
| 1 |
| tanA |
| 1 |
| 2 |
则tanB的最大值为
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:此题考查了同角三角函数间的基本关系,两角和与差的正弦、正切函数公式,以及基本不等式的运用,熟练掌握基本关系及公式是解本题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 )-
)- cos(ωx+
cos(ωx+ )的值;
)的值;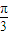 )-
)-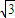 cos(ωx+
cos(ωx+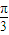 )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π.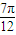 )的值;
)的值;