题目内容
已知正四棱锥S-ABCD中,SA=2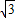 ,那么当该棱锥的体积最大时,它的高为( )
,那么当该棱锥的体积最大时,它的高为( )A.1
B.
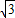
C.2
D.3
【答案】分析:设出底面边长,求出正四棱锥的高,写出体积表达式,利用求导求得最大值时,高的值.
解答:解:设底面边长为a,则高h=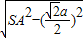 =
=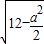 ,所以体积V=
,所以体积V= a2h=
a2h=
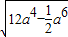 ,
,
设y=12a4- a6,则y′=48a3-3a5,当y取最值时,y′=48a3-3a5=0,解得a=0或a=4时,体积最大,
a6,则y′=48a3-3a5,当y取最值时,y′=48a3-3a5=0,解得a=0或a=4时,体积最大,
此时h=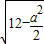 =2,故选C.
=2,故选C.
点评:本试题主要考查椎体的体积,考查高次函数的最值问题的求法.是中档题.
解答:解:设底面边长为a,则高h=
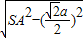 =
=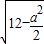 ,所以体积V=
,所以体积V= a2h=
a2h=
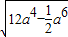 ,
,设y=12a4-
 a6,则y′=48a3-3a5,当y取最值时,y′=48a3-3a5=0,解得a=0或a=4时,体积最大,
a6,则y′=48a3-3a5,当y取最值时,y′=48a3-3a5=0,解得a=0或a=4时,体积最大,此时h=
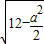 =2,故选C.
=2,故选C.点评:本试题主要考查椎体的体积,考查高次函数的最值问题的求法.是中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 (文做理不做)已知:正四棱锥S-ABCD的高为
(文做理不做)已知:正四棱锥S-ABCD的高为