题目内容
（13分）已知函数
.
(Ⅰ)若
在
上是增函数,求实数
的取值范围；
,使得的导函数
有最大值
?若存在,求出的值;若不存在,请说明理由.
解析：(Ⅰ)由已知得
的定义域为
,
. …………2分
由题意得
对一切
恒成立,
……………………………………………5分
当时,
,
.故
. …………………………………………7分
(Ⅱ)假设存在正实数
,使得
成立.
. …………………9分
由
,得
,
.由于
,故应舍去.
当
时,
………………………………………11分
令
,解得
或
. …………………………13分
另解: 假设存在正实数,使得成立.
设
,则
. ………………………9分
由
,解得
或
.
因为
,
在
上单调递增,在
上单调递减.
. … ……………………………………11分
,解得或. …………………………13分 
练习册系列答案
相关题目
，若
在
＝1处的切线方程为
。 （1） 求
都有
成立，求函数
＝
的最值。
在
上是减函数，求
的最大值；
，求函数y=
的切线与两坐标轴围成图形的面积。
，若
在区间
上的最大值为1，则
的取
，若
在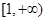
上恒成立，求
的取值范围．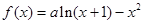
，若在区间（0，1）内任取两个实数p，q，且
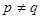，不等式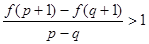
恒成立，则实数a的取值范围是