题目内容
已知函数f(x)=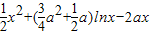 ,a∈R.
,a∈R.(Ⅰ)当a=
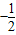 时,求函数f(x)的极值点;
时,求函数f(x)的极值点;(Ⅱ)若函数f(x)在导函数f′(x)的单调区间上也是单调的,求a的取值范围;
(Ⅲ) 当0<a<
 时,设g(x)=f(x)-(
时,设g(x)=f(x)-(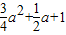 )lnx-(a+
)lnx-(a+ )x2+(2a+1)x,且x1,x2是函数g(x)的极值点,证明:g(x1)+g(x2)>3-2ln2.
)x2+(2a+1)x,且x1,x2是函数g(x)的极值点,证明:g(x1)+g(x2)>3-2ln2.
【答案】分析:(Ⅰ)f(x)= x2-
x2-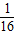 lnx+x,(x>0),f′(x)=x-
lnx+x,(x>0),f′(x)=x-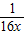 +1=0,由此能求出函数f(x)的极值点.
+1=0,由此能求出函数f(x)的极值点.
(Ⅱ)f′(x)=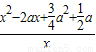 (x>0),令g(x)=x2-2ax+a2+a,△=4a2-3a2-2a=a2-2a,设g(x)=0的两根x1,x2(x1<x2),由此进行分类讨论,能求出a的取值范围.
(x>0),令g(x)=x2-2ax+a2+a,△=4a2-3a2-2a=a2-2a,设g(x)=0的两根x1,x2(x1<x2),由此进行分类讨论,能求出a的取值范围.
(Ⅲ) g(x)=-lnx-ax2+x,g′(x)=-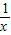 -2ax+1=-
-2ax+1=-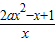 .令g′(x)=0,即2ax2-x+1=0,当0<a<时,△=1-8a>0,所以,方程2ax2-x+1=0的两个不相等的正根x1,x2,设x1<x2,则当x∈(0,x1)∪(x2,+∞)时,g′(x)<0,当x∈(x1,x2)时,g′(x)>0,所以g(x)有极小值点x1和极大值点x2,且x1+x2=
.令g′(x)=0,即2ax2-x+1=0,当0<a<时,△=1-8a>0,所以,方程2ax2-x+1=0的两个不相等的正根x1,x2,设x1<x2,则当x∈(0,x1)∪(x2,+∞)时,g′(x)<0,当x∈(x1,x2)时,g′(x)>0,所以g(x)有极小值点x1和极大值点x2,且x1+x2=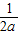 ,x1x2=
,x1x2=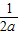 .由此能够证明g(x1)+g(x2)>3-2ln2.
.由此能够证明g(x1)+g(x2)>3-2ln2.
解答:解:(Ⅰ)f(x)= x2-
x2-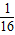 lnx+x (x>0),f′(x)=x-
lnx+x (x>0),f′(x)=x-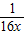 +1=0,
+1=0,
∴x1=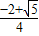 ,x2=
,x2=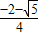 (不在定义域内,舍)
(不在定义域内,舍)
∴(0,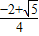 ]单调减,[
]单调减,[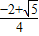 ,+∞)单调增,
,+∞)单调增,
∴f(x)在x=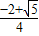 时取极小值,且是唯一极值.
时取极小值,且是唯一极值.
(Ⅱ)f′(x)=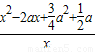 (x>0)
(x>0)
令g(x)=x2-2ax+ a2+
a2+ a,△=4a2-3a2-2a=a2-2a,
a,△=4a2-3a2-2a=a2-2a,
设g(x)=0的两根x1,x2(x1<x2)
1 当△≤0时,即0≤a≤2,f′(x)≥0,
∴f(x)单调递增,满足题意;
2 当△>0时 即a<0或a>2时,
(1)若x1<0<x2,则 a2+a<0,
即-<a<0时,f(x)在(0,x2)上减,(x2,+∞)上增,
f′(x)=x+-2a,f''(x)=1-≥0,
∴f′(x) 在(0,+∞)单调增,不合题意
(2)若x1<x2<0 则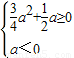 ,
,
即a≤-时f(x)在(0,+∞)上单调增,满足题意.
(3)若0<x1<x2则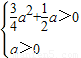 ,
,
即a>2时,∴f(x)在(0,x1)单调增,(x1,x2)单调减,(x2,+∞)单调增,
不合题意.综上得a≤-或0≤a≤2.
(Ⅲ) g(x)=-lnx-ax2+x,g′(x)=-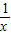 -2ax+1=-
-2ax+1=-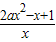 .
.
令g′(x)=0,即2ax2-x+1=0,
当0<a<时,△=1-8a>0,
所以,方程2ax2-x+1=0的两个不相等的正根x1,x2,设x1<x2,
则当x∈(0,x1)∪(x2,+∞)时,g′(x)<0,
当x∈(x1,x2)时,g′(x)>0,
所以g(x)有极小值点x1和极大值点x2,且x1+x2=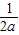 ,x1x2=
,x1x2=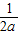 .
.
g(x1)+g(x2)=-lnx1-ax+x1-lnx2-ax+x2
=-(lnx1+lnx2)-(x1-1)-(x2-1)+(x1+x2)
=-ln(x1x2)+(x1+x2)+1
=ln(2a)+…+1.
令h(a)=ln(2a)++1,a∈(0,],
则当a∈(0,)时,h′(a)=-=<0,h(a)在(0,)单调递减,
所以h(a)>h( )=3-2ln2,
)=3-2ln2,
即g(x1)+g(x2)>3-2ln2.
点评:本题考查函数的极值点和实数的取值范围的求法,考查不等式的证明.解题时要认真审题,仔细解答,注意合理地进行等价转化.
 x2-
x2-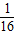 lnx+x,(x>0),f′(x)=x-
lnx+x,(x>0),f′(x)=x-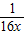 +1=0,由此能求出函数f(x)的极值点.
+1=0,由此能求出函数f(x)的极值点.(Ⅱ)f′(x)=
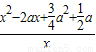 (x>0),令g(x)=x2-2ax+a2+a,△=4a2-3a2-2a=a2-2a,设g(x)=0的两根x1,x2(x1<x2),由此进行分类讨论,能求出a的取值范围.
(x>0),令g(x)=x2-2ax+a2+a,△=4a2-3a2-2a=a2-2a,设g(x)=0的两根x1,x2(x1<x2),由此进行分类讨论,能求出a的取值范围.(Ⅲ) g(x)=-lnx-ax2+x,g′(x)=-
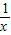 -2ax+1=-
-2ax+1=-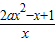 .令g′(x)=0,即2ax2-x+1=0,当0<a<时,△=1-8a>0,所以,方程2ax2-x+1=0的两个不相等的正根x1,x2,设x1<x2,则当x∈(0,x1)∪(x2,+∞)时,g′(x)<0,当x∈(x1,x2)时,g′(x)>0,所以g(x)有极小值点x1和极大值点x2,且x1+x2=
.令g′(x)=0,即2ax2-x+1=0,当0<a<时,△=1-8a>0,所以,方程2ax2-x+1=0的两个不相等的正根x1,x2,设x1<x2,则当x∈(0,x1)∪(x2,+∞)时,g′(x)<0,当x∈(x1,x2)时,g′(x)>0,所以g(x)有极小值点x1和极大值点x2,且x1+x2=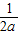 ,x1x2=
,x1x2=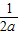 .由此能够证明g(x1)+g(x2)>3-2ln2.
.由此能够证明g(x1)+g(x2)>3-2ln2.解答:解:(Ⅰ)f(x)=
 x2-
x2-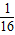 lnx+x (x>0),f′(x)=x-
lnx+x (x>0),f′(x)=x-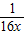 +1=0,
+1=0,∴x1=
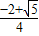 ,x2=
,x2=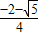 (不在定义域内,舍)
(不在定义域内,舍)∴(0,
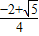 ]单调减,[
]单调减,[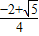 ,+∞)单调增,
,+∞)单调增,∴f(x)在x=
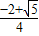 时取极小值,且是唯一极值.
时取极小值,且是唯一极值.(Ⅱ)f′(x)=
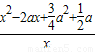 (x>0)
(x>0)令g(x)=x2-2ax+
 a2+
a2+ a,△=4a2-3a2-2a=a2-2a,
a,△=4a2-3a2-2a=a2-2a,设g(x)=0的两根x1,x2(x1<x2)
1 当△≤0时,即0≤a≤2,f′(x)≥0,
∴f(x)单调递增,满足题意;
2 当△>0时 即a<0或a>2时,
(1)若x1<0<x2,则 a2+a<0,
即-<a<0时,f(x)在(0,x2)上减,(x2,+∞)上增,
f′(x)=x+-2a,f''(x)=1-≥0,
∴f′(x) 在(0,+∞)单调增,不合题意
(2)若x1<x2<0 则
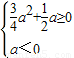 ,
,即a≤-时f(x)在(0,+∞)上单调增,满足题意.
(3)若0<x1<x2则
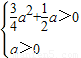 ,
,即a>2时,∴f(x)在(0,x1)单调增,(x1,x2)单调减,(x2,+∞)单调增,
不合题意.综上得a≤-或0≤a≤2.
(Ⅲ) g(x)=-lnx-ax2+x,g′(x)=-
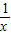 -2ax+1=-
-2ax+1=-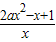 .
.令g′(x)=0,即2ax2-x+1=0,
当0<a<时,△=1-8a>0,
所以,方程2ax2-x+1=0的两个不相等的正根x1,x2,设x1<x2,
则当x∈(0,x1)∪(x2,+∞)时,g′(x)<0,
当x∈(x1,x2)时,g′(x)>0,
所以g(x)有极小值点x1和极大值点x2,且x1+x2=
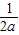 ,x1x2=
,x1x2=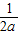 .
.g(x1)+g(x2)=-lnx1-ax+x1-lnx2-ax+x2
=-(lnx1+lnx2)-(x1-1)-(x2-1)+(x1+x2)
=-ln(x1x2)+(x1+x2)+1
=ln(2a)+…+1.
令h(a)=ln(2a)++1,a∈(0,],
则当a∈(0,)时,h′(a)=-=<0,h(a)在(0,)单调递减,
所以h(a)>h(
 )=3-2ln2,
)=3-2ln2,即g(x1)+g(x2)>3-2ln2.
点评:本题考查函数的极值点和实数的取值范围的求法,考查不等式的证明.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|