题目内容
将一颗骰子抛掷两次,第一次出现的点数记为a,第二次出现的点数记为b,设两条直线l1:ax+by-2=0,l2:x+2y-2=0平行的概率为P1,相交的概率为P2,则(P1,P2)所对应的点在直线l2的
下
下
方(填“上”或“下”).分析:先由分步计数原理计算可得直线l1:ax+by-2=0的情况数目,分析两条直线平行与重合的情况数目,可得两直线平行的概率,进而可得两直线相交的概率,得到点P的坐标,将点P的坐标代入方程判定即可.
解答:解:根据题意,分析可得a、b都有6种情况,故直线l1:ax+by-2=0的情况有36种,
设两条直线l1:ax+by=2,l2:x+2y=2平行,即
=
的情况有三种:a=2,b=4,或a=3,b=6,a=1,b=2;
其中a=1,b=2时,两直线重合;a=2,b=4,或a=3,b=6时,两直线平行;
故P1=
,
两直线重合的概率为
,
则两条直线相交的概率P2=1-
-
=
,
(P1,P2)所对应的点为P(
,
),
将(
,
)代入直线x+2y=2方程得2×
<2-
,
即P在l2直线的下方;
故答案为下.
设两条直线l1:ax+by=2,l2:x+2y=2平行,即
| a |
| b |
| 1 |
| 2 |
其中a=1,b=2时,两直线重合;a=2,b=4,或a=3,b=6时,两直线平行;
故P1=
| 1 |
| 18 |
两直线重合的概率为
| 1 |
| 36 |
则两条直线相交的概率P2=1-
| 1 |
| 18 |
| 1 |
| 36 |
| 11 |
| 12 |
(P1,P2)所对应的点为P(
| 1 |
| 18 |
| 11 |
| 12 |
将(
| 1 |
| 18 |
| 11 |
| 12 |
| 11 |
| 12 |
| 1 |
| 18 |
即P在l2直线的下方;
故答案为下.
点评:本题考查等可能事件的概率计算,涉及直线之间的位置关系的判断,注意不要忽略直线重合的情况.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
将一颗骰子抛掷两次分别得到向上的点数a,b,则直线ax-bx=0与圆x2+(y-5)2=5相切的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 ,
, ,则直线
,则直线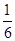 B.
B.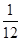 C.
C.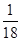 D.
D.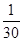
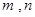 ,则函数
,则函数 在
在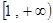 上为增函数的概率是 ( )
上为增函数的概率是 ( )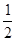 B.
B.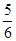 C.
C.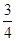 D.
D.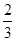
 ,第二次出现的点数记为
,第二次出现的点数记为 ,设两条直线
,设两条直线 ,
, 平行的概率为
平行的概率为 ,相交的概率为
,相交的概率为 ,则
,则 所对应的点在直线
所对应的点在直线 的________方(填“上”或“下”).
的________方(填“上”或“下”).