题目内容
已知命题p:在区间[-1,1]上至少存在一个实数x,使不等式x2+ax-2>0成立;命题q:方程sinx•cosx=a+2,x∈(0,
π]有两个解.若命题“p或q”是真命题,求实数a的取值范围.
| 3 | 4 |
分析:先求出命题p,q的等价条件,然后利用命题“p∨q”是真命题,则命题P、q至少一个为真命题,求a的取值范围.
解答:解:由于在区间[-1,1]上至少存在一个实数x,不等式x2+ax-2>0成立;
令f(x)=x2+ax-2,则f(1)>0或f(-1)>0
解得:a<-1或a>1,
∴命题p为真命题时,a<-1或a>1;
∵a+2=
sin2x,x∈(0,
π]有两个解,
∴0<a+2<
,解得:-2<a<-
∴命题q为真命题时,-2<a<-
由于命题“p或q”是真命题,根据复合命题真值表,命题p、q至少一个为真命题,
①当命题p为真命题q为假命题时,a≤-2或-
≤a<-1或a>1;
②当命题p为假命题q为真命题时,a无解;
③当命题p为真命题也为真命题时,a<-1或a>1;
综上可知,实数a的取值范围为:a<-1或a>1.
令f(x)=x2+ax-2,则f(1)>0或f(-1)>0
解得:a<-1或a>1,
∴命题p为真命题时,a<-1或a>1;
∵a+2=
| 1 |
| 2 |
| 3 |
| 4 |
∴0<a+2<
| 1 |
| 2 |
| 3 |
| 2 |
∴命题q为真命题时,-2<a<-
| 3 |
| 2 |
由于命题“p或q”是真命题,根据复合命题真值表,命题p、q至少一个为真命题,
①当命题p为真命题q为假命题时,a≤-2或-
| 3 |
| 2 |
②当命题p为假命题q为真命题时,a无解;
③当命题p为真命题也为真命题时,a<-1或a>1;
综上可知,实数a的取值范围为:a<-1或a>1.
点评:本题主要考查复合命题的与简单命题的真假应用,将命题进行等价化简是解决此类问题的关键.

练习册系列答案
相关题目
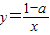 在区间(0,+∞)上是减函数,命题q:不等式(a-2)x2+2(a-2)x-4≥0的解集为空集,若p或q是真命题,求实数a的取值范围.
在区间(0,+∞)上是减函数,命题q:不等式(a-2)x2+2(a-2)x-4≥0的解集为空集,若p或q是真命题,求实数a的取值范围.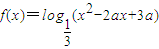 是区间[1,+∞)上的减函数.若命题“p?q”是真命题,求实数a的取值范围.
是区间[1,+∞)上的减函数.若命题“p?q”是真命题,求实数a的取值范围.