题目内容
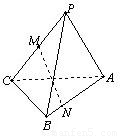
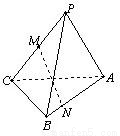
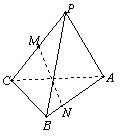 如图,P△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC中点,N是AB上的点,AN=3NB,
如图,P△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC中点,N是AB上的点,AN=3NB,
(1)求证:MN⊥AB;
(2)当∠PAB=90°,BC=2,AB=4时,求MN的长.
解: (1)证明:取AB中点Q,连接PQ,CQ,
(1)证明:取AB中点Q,连接PQ,CQ,
因为CB⊥平面PAB,则PQ⊥BC,又PA=PB,所以PQ⊥AB,
于是PQ⊥平面ABC,所以∠PQC=90°,
因为M是PC中点,所以MQ= PC,
PC,
又因为∠CBP=90°,所以MB= PC,所以MB=MQ;
PC,所以MB=MQ;
而N是BQ的中点,所以MN⊥AB;
(2)当∠APB=90°,BC=2,AB=4时,
有PB=2 ,PC=2
,PC=2 ,MB=
,MB= PC=
PC= ,
,
所以MN= .
.
分析:(1)取AB中点Q,连接PQ,CQ,根据线面垂直的判定定理可知PQ⊥平面ABC,从而∠PQC=90°,再根据M是PC中点,根据直角三角形的中线定理可知MB= PC,则MB=MQ,而N是BQ的中点,根据直角三角形的中线定理可的结论;
PC,则MB=MQ,而N是BQ的中点,根据直角三角形的中线定理可的结论;
(2)先在直角三角形PAB中求出PB,然后求出MB的长以及BN的长,最后在直角三角形MNB中求出MN即可.
点评:本题主要考查了线线的位置关系,以及线段的度量,同时考查了空间想象能力、计算与推理的能力,属于基础题.
 (1)证明:取AB中点Q,连接PQ,CQ,
(1)证明:取AB中点Q,连接PQ,CQ,因为CB⊥平面PAB,则PQ⊥BC,又PA=PB,所以PQ⊥AB,
于是PQ⊥平面ABC,所以∠PQC=90°,
因为M是PC中点,所以MQ=
 PC,
PC,又因为∠CBP=90°,所以MB=
 PC,所以MB=MQ;
PC,所以MB=MQ;而N是BQ的中点,所以MN⊥AB;
(2)当∠APB=90°,BC=2,AB=4时,
有PB=2
 ,PC=2
,PC=2 ,MB=
,MB= PC=
PC= ,
,所以MN=
 .
.分析:(1)取AB中点Q,连接PQ,CQ,根据线面垂直的判定定理可知PQ⊥平面ABC,从而∠PQC=90°,再根据M是PC中点,根据直角三角形的中线定理可知MB=
 PC,则MB=MQ,而N是BQ的中点,根据直角三角形的中线定理可的结论;
PC,则MB=MQ,而N是BQ的中点,根据直角三角形的中线定理可的结论;(2)先在直角三角形PAB中求出PB,然后求出MB的长以及BN的长,最后在直角三角形MNB中求出MN即可.
点评:本题主要考查了线线的位置关系,以及线段的度量,同时考查了空间想象能力、计算与推理的能力,属于基础题.

练习册系列答案
相关题目
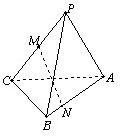 如图,P△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC中点,N是AB上的点,AN=3NB,
如图,P△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC中点,N是AB上的点,AN=3NB, 如图,PA⊥△ABC所在平面,AB=AC=13,BC=10,PA=5,求点P到直线BC的距离.
如图,PA⊥△ABC所在平面,AB=AC=13,BC=10,PA=5,求点P到直线BC的距离.