题目内容
已知函数f(x)=log2(1-x)-log2(1+x)。
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)方程f(x)=x+1是否有根?如果有根x0,请求出一个长度为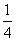 的区间(a,b),使x0∈(a,b);如果没有,请说明理由?(注:区间(a,b)的长度=b-a)
的区间(a,b),使x0∈(a,b);如果没有,请说明理由?(注:区间(a,b)的长度=b-a)
(1)求函数f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)方程f(x)=x+1是否有根?如果有根x0,请求出一个长度为
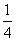 的区间(a,b),使x0∈(a,b);如果没有,请说明理由?(注:区间(a,b)的长度=b-a)
的区间(a,b),使x0∈(a,b);如果没有,请说明理由?(注:区间(a,b)的长度=b-a) 解:(1)要使函数有意义,则 ,∴
,∴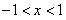 ,
,
故函数的定义域为(-1,1)。
(2)∵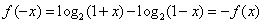 ,
,
∴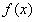 为奇函数。
为奇函数。
(3)由题意,知方程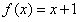 等价于
等价于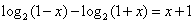 ,
,
可化为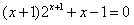 ,
,
设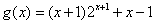 ,x∈(-1,1),
,x∈(-1,1),
则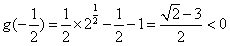 ,
,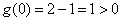 ,
,
所以,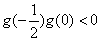 ,故方程在(
,故方程在(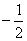 ,0)上必有根,
,0)上必有根,
又因为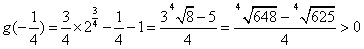 ,
,
所以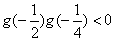 ,
,
故方程在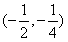 必有一根,
必有一根,
所以,满足题意的一个区间为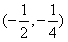 。
。
 ,∴
,∴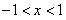 ,
,故函数的定义域为(-1,1)。
(2)∵
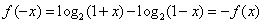 ,
,∴
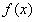 为奇函数。
为奇函数。(3)由题意,知方程
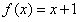 等价于
等价于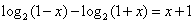 ,
,可化为
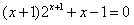 ,
,设
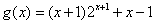 ,x∈(-1,1),
,x∈(-1,1),则
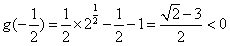 ,
,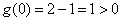 ,
,所以,
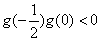 ,故方程在(
,故方程在(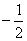 ,0)上必有根,
,0)上必有根,又因为
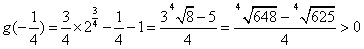 ,
,所以
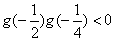 ,
,故方程在
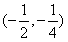 必有一根,
必有一根,所以,满足题意的一个区间为
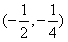 。
。
练习册系列答案
相关题目