题目内容
直线y=kx-1与双曲线x2-y2=1有且只有一个公共点，则k的取值是（ ）
| A、±1 | ||||
B、±
| ||||
C、-1或±
| ||||
D、±
|
分析：用代数法，先联立方程，消元后得到一个方程，先研究相切的情况，即判别式等于零，再研究与渐近线平行的情况．
解答：解：根据题意：
，
消去y整理得（1-k2）x2+2kx-5=0，
∵△=0，
∴k=±
；
又注意直线恒过点（0，-1）且渐近线的斜率为±1，
与渐近线平行时也成立．
故选D．
|
消去y整理得（1-k2）x2+2kx-5=0，
∵△=0，
∴k=±
| ||
| 2 |
又注意直线恒过点（0，-1）且渐近线的斜率为±1，
与渐近线平行时也成立．
故选D．
点评：本题主要考查直线与双曲线的位置关系，在只有一个公共点时，不要忽视了与渐近线平行的情况．
练习册系列答案
相关题目
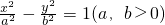的虚轴长为2
，渐近线方程是y=
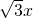，O为坐标原点，直线y=kx+m（k，m∈R）与双曲线C相交于A、B两点，且
．
的虚轴长为2
，渐近线方程是y=
，O为坐标原点，直线y=kx+m（k，m∈R）与双曲线C相交于A、B两点，且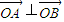
．