题目内容
函数f（x）=xln（x+1）在区间（k-1，k）上不是单调函数，则实数k的取值范围为 ．
考点：利用导数研究函数的单调性
专题：函数的性质及应用,导数的概念及应用
分析：先确定函数的定义域然后求导数fˊ（x），在函数的定义域内解方程fˊ（x）=0，使方程的解在定义域内的一个子区间（k-1，k）内，建立不等关系，解之即可．
解答：
解：因为f（x）定义域为（-1，+∞），
又f′（x）=ln（x+1）+
，
由fˊ（x）=0，得x=0．
当x∈（-1，0）时，fˊ（x）＜0，当x∈（0，+∞）时，fˊ（x）＞0
据题意，
，
解得0＜k＜1．
故答案为：（0，1）．
又f′（x）=ln（x+1）+
| x |
| x+1 |
由fˊ（x）=0，得x=0．
当x∈（-1，0）时，fˊ（x）＜0，当x∈（0，+∞）时，fˊ（x）＞0
据题意，
|
解得0＜k＜1．
故答案为：（0，1）．
点评：本题主要考查了对数函数的导数，以及利用导数研究函数的单调性等基础知识，考查计算能力，属于基础题．
练习册系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
下列说法错误的是（ ）
| A、已知命题p为“?x∈[0，+∞），（log32）x≤1”，则￢p是真命题 |
| B、若p∨q为假命题，则p、q均为假命题 |
| C、x＞2是x＞1充分不必要条件 |
| D、“全等三角形的面积相等”的否命题是假命题 |
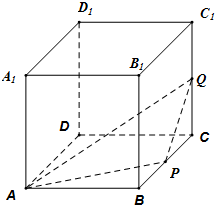正方体ABCD-A1B1C1D1为棱长为1，动点P，Q分别在棱BC，CC1上，过点A，P，Q的平面截该正方体所得的截面记为S，设BP=x，CQ=y，其中x，y∈[0，1]，下列命题正确的是
