题目内容
已知函数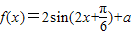
a∈R，a是常数（1）求
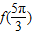的值（2）若函数f（x）在
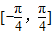上的最大值与最小值之和为
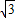，求实数a的值．
【答案】分析：（1）将x=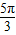
代入f（x）=2sin（2x+
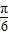）+a，可求得f（
）；
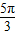（2）由x∈[-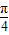
，
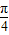]，可求得2x+
∈[-
，
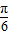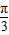]，继而可得sin（2x+
）∈[-
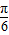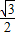，1]，结合题意即可求得a的值．
解答：解：（1）∵f（x）=2sin（2x+
）+a，a∈R，
∴f（
）=2sin（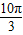
+
）+a=-2+a…（3分）
（2）因为x∈[-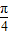
，
]，
∴2x+
∈[-
，
]，
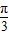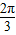∴sin（2x+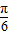
）∈[-
，1]…（6分）
∴-
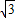+a≤f（x）≤2+a…（9分）
即ymax=2+a，
ymin=-
+a，由已知得-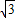
+a+a+2=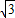
∴a=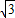
-1…（12分）
点评：本题考查正弦函数的性质，考查分析与运算能力，考查规范书写与表达能力，属于中档题．
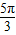代入f（x）=2sin（2x+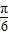）+a，可求得f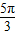（）；（2）由x∈[-
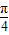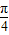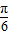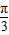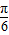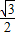，]，可求得2x+∈[-，]，继而可得sin（2x+）∈[-，1]，结合题意即可求得a的值．解答：解：（1）∵f（x）=2sin（2x+
）+a，a∈R，∴f（
）=2sin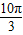（+）+a=-2+a…（3分）（2）因为x∈[-
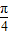，]，∴2x+
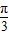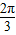∈[-，]，∴sin（2x+
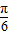）∈[-，1]…（6分）∴-
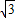+a≤f（x）≤2+a…（9分）即ymax=2+a，
ymin=-
+a，由已知得-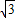+a+a+2=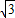∴a=
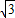-1…（12分）点评：本题考查正弦函数的性质，考查分析与运算能力，考查规范书写与表达能力，属于中档题．
练习册系列答案
相关题目
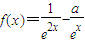，其中a∈R．
，若g（x）的图象恒在直线y=e上方，求实数a的取值范围（其中e为自然对数的底数，e=2.71828…）．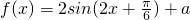
a∈R，a是常数
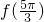的值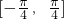
上的最大值与最小值之和为
，求实数a的值．