题目内容
【题目】如图1，在边长为 
的正方形ABCD中，E、O分别为 AD、BC的中点，沿 EO将矩形ABOE折起使得∠BOC=120°，如图2所示，点G 在BC上，BG=2GC，M、N分别为AB、EG中点．
（Ⅰ）求证：MN∥平面OBC；
（Ⅱ）求二面角 G﹣ME﹣B的余弦值．
【答案】证明：（Ⅰ）法一如图13取OG中点F，连结BF、FN，
则中位线FN∥ 
OE且FN= OE，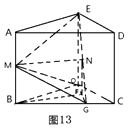
又BM∥ OE且BM= OE
所以FN∥BM且FN=BM，所以四边形BFNM是平行四边形，所以MN∥BF，
又MN平面OBC，BF平面OBC，所以MN∥平面OBC
法二：如图14，延长EM、OB交于点Q，连结GQ，
因为BM∥OE且BM=OE，所以 
，
M为EQ中点，
所以中位线MN∥QG
又MN平面OBC，QG面OBC，所以MN∥平面OBC．
（Ⅱ）解：
法一如图14，因为OB=OC= 
，∠BOC=120°，
所以 
，
又BG=2GC．所以 
， 
，
∴OB2+OG2=BG2 ， ∴∠BOG=90°，OG⊥OB，
又∵OE⊥OB，OE⊥OC，OB∩OC=O，
∴OE⊥平面OBC，OG面OBC，
∴OE⊥OG
又OB∩OE=O，所以OG⊥平面OBE，QE面OBE OG⊥QE，
又M为EQ中点，所以OQ=OE= 
，所以OM⊥QE，OM∩OG=O，
所以QE⊥平面OMG，QE⊥MG，∠OMG为二面角G﹣ME﹣B的平面角．
所以Rt△MOG中， 
， 
， 
，∴二面角 G﹣ME﹣B的余弦值为 
法二：如图，∵OB=OC= ，∠BOC=120°，
∴
又BG=2GC，∴ ， ，
∴OB2+OG2=BG2 ，
∴∠BOG=90°，OG⊥OB，
又∵OE⊥OB，OE⊥OC，OB∩OC=O，
∴OE⊥平面OBC，OG面OBC，
∴OE⊥OG
又OB∩OE=O，所以OG⊥平面OBE，OE面OBE，∴OG⊥OE
建立如图所示的空间直角坐标系O﹣xyz，则M（ 
，G（0，1，0），E 
， 
，
而 
是平面BOE的一个法向量，
设平面MGE的法向量为 
，
则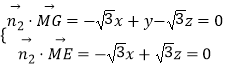 
，
令 z=1，则 
，
面MGE的一个法向量为 
，
所以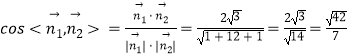 
所以，二面角 G﹣ME﹣B的余弦值为 
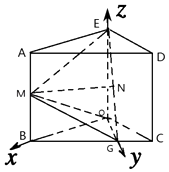
【解析】（Ⅰ）法一：取OG中点F，连结BF、FN，证明MN∥BF，然后证明MN∥平面OBC．法二：延长EM、OB交于点Q，连结GQ，证明M为EQ中点，推出MN∥QG，然后证明MN∥平面OBC．（Ⅱ）法一：证明OG⊥OB，推出OE⊥平面OBC，证明OE⊥OG，然后推出OG⊥QE，说明∠OMG为二面角G﹣ME﹣B的平面角，Rt△MOG中，求解即可．法二：建立空间直角坐标系O﹣xyz，求出面BOE的一个法向量，平面MGE的法向量，利用空间向量的数量积求解即可．
【考点精析】根据题目的已知条件，利用直线与平面平行的判定的相关知识可以得到问题的答案，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
