题目内容
已知直线![]() 经过椭圆
经过椭圆![]() 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆![]() 的右顶点为
的右顶点为![]() ,点
,点![]() 和椭圆
和椭圆![]() 上位于
上位于![]() 轴上方的动点,直线,
轴上方的动点,直线,![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点。
两点。
(I)求椭圆![]() 的方程;(Ⅱ)求线段MN的长度的最小值;
的方程;(Ⅱ)求线段MN的长度的最小值;
(Ⅲ)当线段MN的长度最小时,在椭圆![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() 的面积为
的面积为![]() ?若存在,确定点
?若存在,确定点![]() 的个数,若不存在,说明理由
的个数,若不存在,说明理由
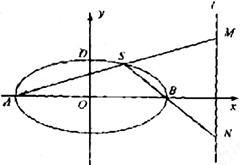
解法一:
(I)由已知得,椭圆![]() 的左顶点为
的左顶点为![]() 上顶点为
上顶点为![]()
故椭圆![]() 的方程为
的方程为![]()
(Ⅱ)直线AS的斜率![]() 显然存在,且
显然存在,且![]() ,故可设直线
,故可设直线![]() 的方程为
的方程为![]() ,从而
,从而![]()
由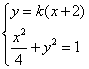 得
得![]() 0
0
设![]() 则
则![]() 得
得![]() ,从而
,从而![]()
即![]() 又
又![]()
由 得
得
![]()
故![]()
又![]()
当且仅当![]() ,即
,即![]() 时等号成立
时等号成立
![]() 时,线段
时,线段![]() 的长度取最小值
的长度取最小值![]()
(Ⅲ)由(Ⅱ)可知,当![]() 取最小值时,
取最小值时,![]()
此时![]() 的方程为
的方程为![]()
要使椭圆![]() 上存在点
上存在点![]() ,使得
,使得![]() 的面积等于
的面积等于![]() ,只须
,只须![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,所以
,所以![]() 在平行于
在平行于![]() 且与
且与![]() 距离等于
距离等于![]() 的直线
的直线![]() 上。
上。
设直线![]()
则由![]() 解得
解得![]() 或
或![]()

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目

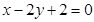 经过椭圆
经过椭圆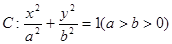 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆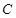 的右顶点为
的右顶点为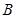 ,点
,点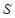 是椭圆
是椭圆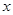 轴上方的动点,直线
轴上方的动点,直线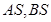 与直线
与直线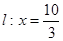 分别交于
分别交于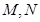 两点。
两点。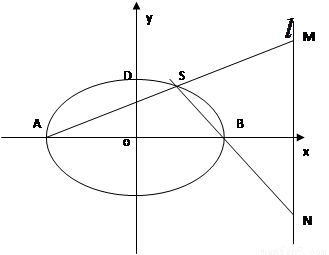
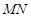 的长度的最小值;
的长度的最小值;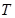 ,使得
,使得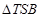 的面积为
的面积为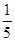 ?若存在,确定点
?若存在,确定点 经过椭圆
经过椭圆 的左顶点
的左顶点 和上顶点
和上顶点 椭圆
椭圆 的右顶点为
的右顶点为 ,点
,点 是椭圆
是椭圆 轴上方的动点,直线
轴上方的动点,直线 与直线
与直线 分别交于
分别交于 两点,如图所示。
两点,如图所示。 的长度的最小值;
的长度的最小值; ,使得
,使得 的面积
的面积 ?若存在,确定点
?若存在,确定点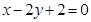 经过椭圆
经过椭圆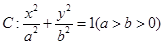 的左顶点
的左顶点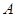 和上顶点
和上顶点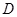 ,椭圆
,椭圆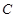 的右顶点为
的右顶点为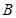 ,点
,点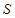 是椭圆
是椭圆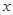 轴上方的动点,直线
轴上方的动点,直线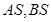 与直线
与直线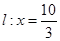 分别交于
分别交于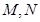 两点.
两点.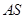 与直线
与直线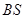 斜率的乘积为定值;
斜率的乘积为定值;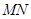 的长度的最小值.
的长度的最小值.