题目内容
已知椭圆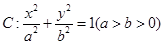 过点
过点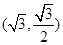 ,椭圆
,椭圆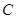 左右焦点分别为
左右焦点分别为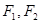 ,上顶点为
,上顶点为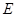 ,
,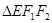 为等边三角形.定义椭圆C上的点
为等边三角形.定义椭圆C上的点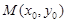 的“伴随点”为
的“伴随点”为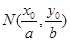 .
.
(1)求椭圆C的方程;
(2)求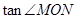 的最大值;
的最大值;
(3)直线l交椭圆C于A、B两点,若点A、B的“伴随点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.椭圆C的右顶点为D,试探究ΔOAB的面积与ΔODE的面积的大小关系,并证明.
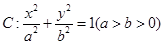 过点
过点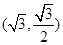 ,椭圆
,椭圆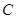 左右焦点分别为
左右焦点分别为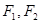 ,上顶点为
,上顶点为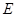 ,
,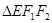 为等边三角形.定义椭圆C上的点
为等边三角形.定义椭圆C上的点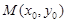 的“伴随点”为
的“伴随点”为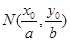 .
.(1)求椭圆C的方程;
(2)求
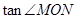 的最大值;
的最大值;(3)直线l交椭圆C于A、B两点,若点A、B的“伴随点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.椭圆C的右顶点为D,试探究ΔOAB的面积与ΔODE的面积的大小关系,并证明.
(1) (2)
(2) (3)
(3) 的面积是定值
的面积是定值
 (2)
(2) (3)
(3) 的面积是定值
的面积是定值
试题分析:解:(1)由已知
 ,解得
,解得 ,方程为
,方程为 .4分
.4分 (2)当
 时,显然
时,显然 ,由椭圆对称性,只研究
,由椭圆对称性,只研究 即可,
即可,设
 (
( ),于是
),于是 5分
5分 (当且仅当
(当且仅当 时取等号) 8分
时取等号) 8分(3) 设
 ,则
,则 ;
; 1)当直线
 的斜率存在时,设方程为
的斜率存在时,设方程为 ,
, 由
 得:
得:  ;
; 有
 ① 10分
① 10分由以
 为直径的圆经过坐标原点O可得:
为直径的圆经过坐标原点O可得:  ;
;整理得:
 ②
②将①式代入②式得:
 , 12分
, 12分 
又点
 到直线
到直线 的距离
的距离
 =
= =
= =
=
所以
 14分
14分 2) 当直线
 的斜率不存在时,设方程为
的斜率不存在时,设方程为
联立椭圆方程得:
 ;
;代入
 得
得 ;
; ,
,

综上:
 的面积是定值
的面积是定值
又
 的面积也为
的面积也为 ,所以二者相等. 16分
,所以二者相等. 16分点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
相关题目
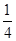



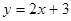 与抛物线
与抛物线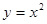 所围成的图形面积是( )
所围成的图形面积是( )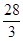
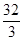
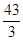
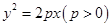 的准线经过椭圆
的准线经过椭圆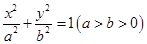 的左焦点,且经过抛物线与椭圆两个交点的弦过抛物线的焦点,则椭圆的离心率为_____________
的左焦点,且经过抛物线与椭圆两个交点的弦过抛物线的焦点,则椭圆的离心率为_____________ ,
, 为双曲线
为双曲线 的右焦点,点
的右焦点,点 ,
, 为
为 轴正半轴上的动点。
轴正半轴上的动点。 的最大值为( )
的最大值为( )



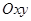 中,若双曲线
中,若双曲线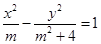 的焦距为8,则
的焦距为8,则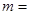
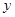 轴上,渐近线方程为
轴上,渐近线方程为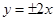 的双曲线的离心率为_______.
的双曲线的离心率为_______.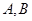 是椭圆
是椭圆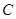 :
: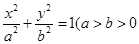 且
且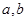 为常数
为常数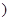 上关于原点对称的两点,点
上关于原点对称的两点,点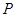 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线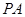 和
和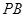 的斜率都存在,并分别记为
的斜率都存在,并分别记为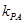 ,
,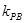 ,那么
,那么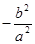 .
.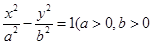 且
且