题目内容
已知函数f(x)=lnx-ax.
(1)当a=1时,求f(x)的最大值;
(2)试讨论函数y=f(x)的零点情况;
(3)设ak,bk,…(k=1,2,…,n)均为正数,若a1b1+a2b2+…+anbn≤b1+b2+…+bn,求证: …
… ≤1.
≤1.
解:(1)当a=1时,f′(x)= -1,当x>1时,f′(x)<0,当0<x<1时,f′(x)>0.
-1,当x>1时,f′(x)<0,当0<x<1时,f′(x)>0.
故函数f(x)=lnx-ax在(0,1)上是增函数,在(1,+∞)上是减函数.
故fmax(x)=f(1)=ln1-1=-1.
(2)由 y=f(x)=0 可得lnx=ax,故函数y=f(x)的零点个数即为 y=lnx与 y=ax 的交点的个数.
结合图象可得,当a≤0时,f(x)的零点个数仅有一个.
当a>0时,令f′(x)= -a=0,可得 x=
-a=0,可得 x= .
.
由于 当x> 时,f′(x)<0,当0<x<
时,f′(x)<0,当0<x< 时,f′(x)>0. 故 f(x)在(0,
时,f′(x)>0. 故 f(x)在(0, )上是增函数,在(
)上是增函数,在( ,+∞)上是减函数.
,+∞)上是减函数.
故fmax(x)=f( )=-lna-1.
)=-lna-1.
故当-lna-1>0时,即 0<a< 时,y=f(x)有2个零点;当a=
时,y=f(x)有2个零点;当a= 时,y=f(x)有1个零点; 当a>
时,y=f(x)有1个零点; 当a> 时,y=f(x)没有零点.
时,y=f(x)没有零点.
综上可得,当a≤0或a= 时,y=f(x)有1个零点; 当 0<a<
时,y=f(x)有1个零点; 当 0<a< 时,y=f(x)有2个零点; 当a>
时,y=f(x)有2个零点; 当a> 时,y=f(x)没有零点.
时,y=f(x)没有零点.
(3)由(1)可得,当x∈(0,+∞)时,lnx≤x-1.
∵ak,bk 都是正数,∴lnak<ak-1,
∴bk•lnak<bk(ak-1)=bk•ak-bk.
∴ln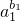 +ln
+ln 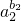 +…+ln
+…+ln 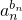 <a1b1+a2b2+…+anbn -( b1+b2+…+bn).
<a1b1+a2b2+…+anbn -( b1+b2+…+bn).
又因为 a1b1+a2b2+…+anbn≤b1+b2+…+bn,
∴ln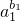 +ln
+ln 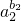 +…+ln
+…+ln 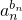 ≤0,即ln(
≤0,即ln(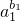 •
•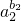 …
…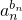 )≤0,
)≤0,
故 …
… ≤1.
≤1.
分析:(1)利用导数研究函数的单调性,可得函数f(x)=lnx-ax在(0,1)上是增函数,在(1,+∞)上是减函数,故fmax(x)=f(1).
(2)由 y=f(x)=0 可得lnx=ax,故函数y=f(x)的零点个数即为 y=lnx与 y=ax 的交点的个数.结合图象可得,当a≤0或a= 时,y=f(x)有1个零点; 当 0<a<
时,y=f(x)有1个零点; 当 0<a< 时,y=f(x)有2个零点; 当a>
时,y=f(x)有2个零点; 当a> 时,y=f(x)没有零点.
时,y=f(x)没有零点.
(3)由(1)可得,当x∈(0,+∞)时,lnx≤x-1,可得 lnak<ak-1,故 bk•lnak<bk(ak-1)=bk•ak-bk.可得 ln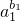 +ln
+ln 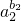 +…+ln
+…+ln 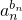 <a1b1+a2b2+…+anbn -( b1+b2+…+bn),再由已知条件证得
<a1b1+a2b2+…+anbn -( b1+b2+…+bn),再由已知条件证得  …
… ≤1成立.
≤1成立.
点评:本题主要考查方程的根的存在性及个数判断,利用导数研究函数的单调性,用放缩法证明不等式,属于中档题.
 -1,当x>1时,f′(x)<0,当0<x<1时,f′(x)>0.
-1,当x>1时,f′(x)<0,当0<x<1时,f′(x)>0.故函数f(x)=lnx-ax在(0,1)上是增函数,在(1,+∞)上是减函数.
故fmax(x)=f(1)=ln1-1=-1.
(2)由 y=f(x)=0 可得lnx=ax,故函数y=f(x)的零点个数即为 y=lnx与 y=ax 的交点的个数.
结合图象可得,当a≤0时,f(x)的零点个数仅有一个.
当a>0时,令f′(x)=
 -a=0,可得 x=
-a=0,可得 x= .
.由于 当x>
 时,f′(x)<0,当0<x<
时,f′(x)<0,当0<x< 时,f′(x)>0. 故 f(x)在(0,
时,f′(x)>0. 故 f(x)在(0, )上是增函数,在(
)上是增函数,在( ,+∞)上是减函数.
,+∞)上是减函数.故fmax(x)=f(
 )=-lna-1.
)=-lna-1.故当-lna-1>0时,即 0<a<
 时,y=f(x)有2个零点;当a=
时,y=f(x)有2个零点;当a= 时,y=f(x)有1个零点; 当a>
时,y=f(x)有1个零点; 当a> 时,y=f(x)没有零点.
时,y=f(x)没有零点.综上可得,当a≤0或a=
 时,y=f(x)有1个零点; 当 0<a<
时,y=f(x)有1个零点; 当 0<a< 时,y=f(x)有2个零点; 当a>
时,y=f(x)有2个零点; 当a> 时,y=f(x)没有零点.
时,y=f(x)没有零点.(3)由(1)可得,当x∈(0,+∞)时,lnx≤x-1.
∵ak,bk 都是正数,∴lnak<ak-1,
∴bk•lnak<bk(ak-1)=bk•ak-bk.
∴ln
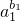 +ln
+ln 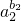 +…+ln
+…+ln 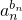 <a1b1+a2b2+…+anbn -( b1+b2+…+bn).
<a1b1+a2b2+…+anbn -( b1+b2+…+bn).又因为 a1b1+a2b2+…+anbn≤b1+b2+…+bn,
∴ln
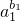 +ln
+ln 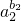 +…+ln
+…+ln 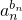 ≤0,即ln(
≤0,即ln(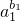 •
•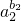 …
…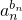 )≤0,
)≤0,故
 …
… ≤1.
≤1.分析:(1)利用导数研究函数的单调性,可得函数f(x)=lnx-ax在(0,1)上是增函数,在(1,+∞)上是减函数,故fmax(x)=f(1).
(2)由 y=f(x)=0 可得lnx=ax,故函数y=f(x)的零点个数即为 y=lnx与 y=ax 的交点的个数.结合图象可得,当a≤0或a=
 时,y=f(x)有1个零点; 当 0<a<
时,y=f(x)有1个零点; 当 0<a< 时,y=f(x)有2个零点; 当a>
时,y=f(x)有2个零点; 当a> 时,y=f(x)没有零点.
时,y=f(x)没有零点.(3)由(1)可得,当x∈(0,+∞)时,lnx≤x-1,可得 lnak<ak-1,故 bk•lnak<bk(ak-1)=bk•ak-bk.可得 ln
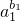 +ln
+ln 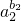 +…+ln
+…+ln 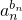 <a1b1+a2b2+…+anbn -( b1+b2+…+bn),再由已知条件证得
<a1b1+a2b2+…+anbn -( b1+b2+…+bn),再由已知条件证得  …
… ≤1成立.
≤1成立.点评:本题主要考查方程的根的存在性及个数判断,利用导数研究函数的单调性,用放缩法证明不等式,属于中档题.

练习册系列答案
相关题目