题目内容
阅读与理解:asinx+bcosx=| a2+b2 |
我们可以根据公式将函数g(x)=sinx+
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
(1)根据你的理解将函数f(x)=
| 3 |
| 2 |
| ||
| 2 |
(2)求出上面函数f(x)的最小正周期、对称中心及单调递增区间.
分析:(1)按阅读材料中的模式提取
,再用正弦的和角公式化简即可
(2)由三函数的相关公式及正弦函数的图象求其单调区间,利用T=
周期,根据正弦函数图象求对称中心的坐标即可
| 3 |
(2)由三函数的相关公式及正弦函数的图象求其单调区间,利用T=
| 2π |
| ω |
解答:解:①由题意f(x)=
sinx+
cosx=
(
sinx+
cosx)=
sin(x+
)
②由①中的解析式知:T=2π,
中心(kπ-
,0),(k∈Z),
令x+
∈ [2kπ-
,2kπ+
] , k∈z
解得,函数的递增区间[2kπ-
,2kπ+
],(k∈Z)
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
②由①中的解析式知:T=2π,
中心(kπ-
| π |
| 6 |
令x+
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
解得,函数的递增区间[2kπ-
| 2π |
| 3 |
| π |
| 3 |
点评:本题考查三角函数恒等变换公式以及正弦函数的图象与性质,属于三角函数中的基础题,利用和差角公式化简三角函数解析式是三角函数中的一个重要运用,要熟练掌握这一公式,了解其用途.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
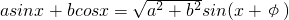 给出公式:
给出公式: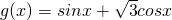 化为:
化为: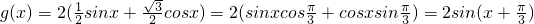
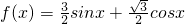 化为f(x)=Asin(ωx+φ)的形式.
化为f(x)=Asin(ωx+φ)的形式. cosx化为:g(x)=2(
cosx化为:g(x)=2( sinx+
sinx+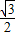 cosx)=2(sinxcos
cosx)=2(sinxcos +cosxsin
+cosxsin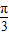 )=2sin(x+
)=2sin(x+ )
) )化为f(x)=Asin(ωx+φ)的形式.
)化为f(x)=Asin(ωx+φ)的形式.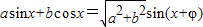 给出公式:
给出公式: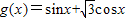 化为:
化为: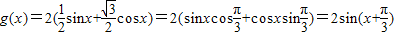
 化为f(x)=Asin(ωx+φ)的形式.
化为f(x)=Asin(ωx+φ)的形式.