题目内容
若集合M={y|y=x2,x∈Z}, ,则M∩N的真子集的个数是________.
,则M∩N的真子集的个数是________.
7
分析:解不等式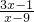 ≤1可得集合N,分析可得集合M={0,1,4,9,16,…,n2,…},其中n是整数,由交集的定义可得M∩N={0,1,4},由集合的元素个数与子集的个数的关系,即可得答案.
≤1可得集合N,分析可得集合M={0,1,4,9,16,…,n2,…},其中n是整数,由交集的定义可得M∩N={0,1,4},由集合的元素个数与子集的个数的关系,即可得答案.
解答: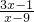 ≤1?
≤1? ≤0,
≤0,
解可得-4≤x<9,则N={x|-4≤x<9},
集合M={0,1,4,9,16,…,n2,…},其中n是整数,
则M∩N={0,1,4},有3个元素,
那么M∩N的真子集的个数是23-1=7;
故答案为7.
点评:本题考查集合的交集运算以及元素与子集的个数关系,要注意集合M的元素为整数,以及正确求解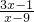 ≤1.
≤1.
分析:解不等式
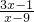 ≤1可得集合N,分析可得集合M={0,1,4,9,16,…,n2,…},其中n是整数,由交集的定义可得M∩N={0,1,4},由集合的元素个数与子集的个数的关系,即可得答案.
≤1可得集合N,分析可得集合M={0,1,4,9,16,…,n2,…},其中n是整数,由交集的定义可得M∩N={0,1,4},由集合的元素个数与子集的个数的关系,即可得答案.解答:
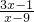 ≤1?
≤1? ≤0,
≤0,解可得-4≤x<9,则N={x|-4≤x<9},
集合M={0,1,4,9,16,…,n2,…},其中n是整数,
则M∩N={0,1,4},有3个元素,
那么M∩N的真子集的个数是23-1=7;
故答案为7.
点评:本题考查集合的交集运算以及元素与子集的个数关系,要注意集合M的元素为整数,以及正确求解
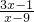 ≤1.
≤1. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
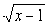 },则M∩P等于 ( )
},则M∩P等于 ( ) ,则M∩P=( )
,则M∩P=( ) ,则M∩P=( )
,则M∩P=( ) ,则M∩P=( )
,则M∩P=( )