题目内容
【题目】四棱柱![]() 的底面是菱形,
的底面是菱形,![]() 平面
平面![]() ,点
,点![]() 是侧棱
是侧棱![]() 上的点
上的点![]()
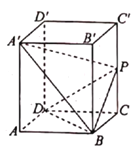
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求四棱锥
的中点,求四棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析(2)![]()
【解析】
(1)要证![]() 平面
平面![]() ,即证
,即证![]() 垂直于平面
垂直于平面![]() 内两条相交直线,题中已知
内两条相交直线,题中已知![]() ,故只要证
,故只要证![]() 垂直于平面
垂直于平面![]() 内另一条与
内另一条与![]() 相交的直线即可,由题意可证出
相交的直线即可,由题意可证出![]() ,从而得证本题;
,从而得证本题;
(2)要求四棱锥![]() 的体积,即求出点
的体积,即求出点![]() 到平面
到平面![]() 的距离和四边形
的距离和四边形![]() 的面积,点
的面积,点![]() 到平面
到平面![]() 的距离即为菱形的高,四边形
的距离即为菱形的高,四边形![]() 是长方形,利用勾股定理可得出
是长方形,利用勾股定理可得出![]() 的长,从而可得出体积。
的长,从而可得出体积。
(1)证明:连接![]() .
.
由![]() 平面
平面![]() ,
,
得![]() .
.
又底面![]() 是菱形,
是菱形,
所以![]() .
.
因为![]() 是平面
是平面![]() 内的相交直线,
内的相交直线,
所以![]() 平面
平面![]() 。
。
又![]() 平面
平面![]() ,
,
所以![]()
又![]() ,
,
所以![]() 平面
平面![]()
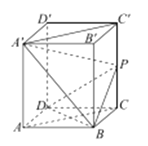
(2)解:连接![]() .
.
当![]() 是
是![]() 中点时,设
中点时,设![]() ,则
,则![]() .
.
在![]() 中,
中,![]() ,
,
故![]()
![]()
![]() ,
,
又![]() ,
,
所以![]() ,
,
即![]()
即![]() 。
。
故侧面![]() 的面积为
的面积为![]() ,
,
点![]() 到平面
到平面![]() 的距离就是底面菱形的高
的距离就是底面菱形的高![]() ,
,
即![]() ,
,
所以四棱锥![]() 的体积为
的体积为![]() 。
。

练习册系列答案
相关题目
【题目】某县畜牧技术员张三和李四![]() 年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量
年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量![]() (单位:万只)与相应年份
(单位:万只)与相应年份![]() (序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系.
(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系.
年份序号 |
|
|
|
|
|
|
|
|
|
年养殖山羊 |
|
|
|
|
|
|
|
|
|
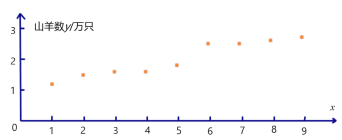
(1)根据表中的数据和所给统计量,求![]() 关于
关于![]() 的线性回归方程(参考统计量:
的线性回归方程(参考统计量:![]() ,
,![]() ;
;
(2)李四提供了该县山羊养殖场的个数![]() (单位:个)关于
(单位:个)关于![]() 的回归方程
的回归方程![]() .
.
试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:![]()
![]()
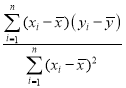 ,
,![]() .
.