题目内容
7.已知边长为3的等边三角形ABC的三个顶点都在以O为球心的球面上,若三棱锥O-ABC的体积为$\frac{3}{2}$$\sqrt{3}$,则球的表面积为28π.分析 由正弦定理求出等边三角形外接圆的半径,再利用三棱锥O-ABC的体积为$\frac{3}{2}$$\sqrt{3}$,求出球半径,由此能求出球的表面积.
解答 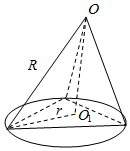 解:设△ABC的外接圆的半径为r,
解:设△ABC的外接圆的半径为r,
∵边长为3的等边三角形ABC的三个顶点都在以O为球心的球面上,
∴由正弦定理得$\frac{3}{sin60°}$=2r,解得r=$\sqrt{3}$,
设△ABC处接圆的圆心为O1,则OO1⊥平面ABC,
∴VO-ABC=$\frac{1}{3}{S}_{△ABC}×O{O}_{1}$=$\frac{1}{3}×(\frac{1}{2}×3×3×sin60°)×O{O}_{1}$=$\frac{3\sqrt{3}}{2}$,
解得OO1=2,
∴球O的半径R=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$,
∴球的表面积为S=4πR2=4π×7=28π.
故答案为:28π.
点评 本题考查球的表面积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
18. 一个几何体的三视图如图所示,则这个几何体的体积为( )
一个几何体的三视图如图所示,则这个几何体的体积为( )
 一个几何体的三视图如图所示,则这个几何体的体积为( )
一个几何体的三视图如图所示,则这个几何体的体积为( )| A. | 20 | B. | 25 | C. | 30 | D. | 40 |
2.曲线y=$\frac{2}{x}$与直线y=x-1及直线x=1所围成的封闭图形的面积为( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{2}$ | C. | 4-2ln2 | D. | 2ln2$-\frac{1}{2}$ |
 中,点
中,点 为
为 的中点,
的中点, ,
, ,则
,则 ( )
( ) B.
B.
 D.
D.