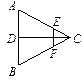题目内容
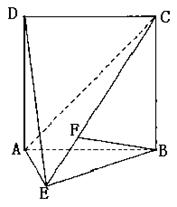
如图,二面角D—AB—E的大小为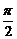 ,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
⑴求证AE⊥平面BCE;
⑵求二面角B—AC—E的正弦值;
⑶求点D到平面ACE的距离.
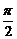 ,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.⑴求证AE⊥平面BCE;
⑵求二面角B—AC—E的正弦值;
⑶求点D到平面ACE的距离.

(1)见解析(2)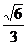 (3)
(3)
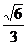 (3)
(3)
(1)易得BC垂直平面ABE,则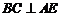
BF垂直平面ACE,所以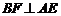
所以AE垂直平面BCD。…………..4’
(2)取AC中点O,连接BO,OF,易得
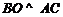 ,再由BF垂直平面ACE得
,再由BF垂直平面ACE得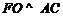 ,
,
所以角BOF即为二面角B—AC—E的平面角或其
补角。…………………………………………..2’
AE垂直BE,所以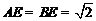 ,则
,则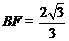 ,又
,又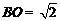 ,所以二面角B—AC—E的正弦值为
,所以二面角B—AC—E的正弦值为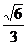 ……………………………………..3’
……………………………………..3’
(3)解一:易知E到平面ACD的距离d就是E到AB的距离,即d=1
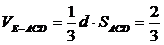 ………………………………….2’
………………………………….2’
设D到平面ACE的距离为h,则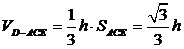 ……...2’
……...2’
可得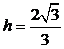 ,即D到平面ACE的距离为
,即D到平面ACE的距离为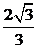 …………………….1’
…………………….1’
解二:因为B、D两点关于直线AC对称,所以BD连线中点在平面ACE上,易得B、D两点到平面ACE的距离相等。………………………3’
B到平面ACE的距离即BF长为 ,
,
所以D到平面ACE的距离为 ……………………….……………….
……………………….……………….
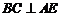
BF垂直平面ACE,所以
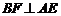
所以AE垂直平面BCD。…………..4’
(2)取AC中点O,连接BO,OF,易得
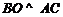 ,再由BF垂直平面ACE得
,再由BF垂直平面ACE得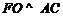 ,
,所以角BOF即为二面角B—AC—E的平面角或其
补角。…………………………………………..2’
AE垂直BE,所以
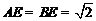 ,则
,则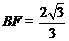 ,又
,又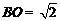 ,所以二面角B—AC—E的正弦值为
,所以二面角B—AC—E的正弦值为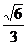 ……………………………………..3’
……………………………………..3’(3)解一:易知E到平面ACD的距离d就是E到AB的距离,即d=1
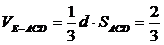 ………………………………….2’
………………………………….2’设D到平面ACE的距离为h,则
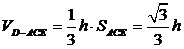 ……...2’
……...2’可得
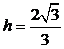 ,即D到平面ACE的距离为
,即D到平面ACE的距离为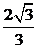 …………………….1’
…………………….1’解二:因为B、D两点关于直线AC对称,所以BD连线中点在平面ACE上,易得B、D两点到平面ACE的距离相等。………………………3’
B到平面ACE的距离即BF长为
 ,
,所以D到平面ACE的距离为
 ……………………….……………….
……………………….……………….
练习册系列答案
相关题目
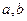 公垂线段
公垂线段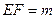 ,线段
,线段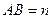 ,
,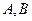 分别在
分别在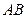 中点轨迹
中点轨迹 的底面为直角梯形,
的底面为直角梯形, ,
, ,
, ,
, ,
, 底面
底面 ,
, 为
为 的中点.
的中点. 平面
平面 ;
; 与平面
与平面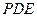 所成的角;
所成的角; 到平面
到平面
 的垂直平分线分别交AB,AC于E,E(图一),沿DE将△ADE折起,使得平面ADE⊥平面BDEC(图二)
的垂直平分线分别交AB,AC于E,E(图一),沿DE将△ADE折起,使得平面ADE⊥平面BDEC(图二)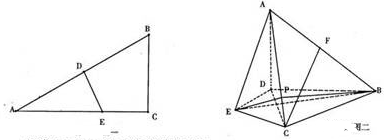
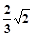
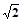
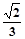
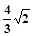
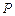 是边长为
是边长为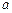 的正
的正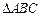 内的一点,
内的一点,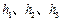 ,则
,则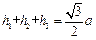 ;类比到空间,设
;类比到空间,设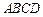 内的一点,则
内的一点,则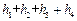 = .
= .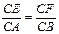 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).