题目内容
对于函数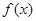 ,若在定义域存在实数
,若在定义域存在实数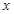 ,满足
,满足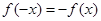 ,则称
,则称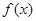 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数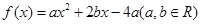 ,试判断
,试判断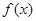 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设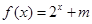 是定义在
是定义在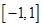 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数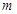 的取值范围.
的取值范围.
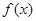 ,若在定义域存在实数
,若在定义域存在实数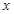 ,满足
,满足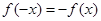 ,则称
,则称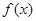 为“局部奇函数”.
为“局部奇函数”.(1)已知二次函数
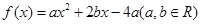 ,试判断
,试判断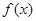 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;(2)设
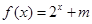 是定义在
是定义在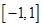 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数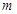 的取值范围.
的取值范围.(1)是“局部奇函数”;(2)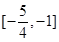 .
.
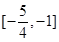 .
.试题分析:(1)本题实质就是解方程
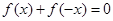 ,如果这个方程有实数解,就说明
,如果这个方程有实数解,就说明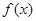 是“局部奇函数”,如果这个方程无实数解,就说明
是“局部奇函数”,如果这个方程无实数解,就说明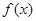 不是“局部奇函数”,易知
不是“局部奇函数”,易知 有实数解,因此答案是肯定的;(2)已经明确
有实数解,因此答案是肯定的;(2)已经明确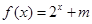 是“局部奇函数”,也就是说方程
是“局部奇函数”,也就是说方程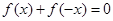 一定有实数解,问题也就变成方程
一定有实数解,问题也就变成方程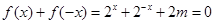 在
在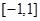 上有解,求参数
上有解,求参数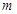 的取值范围,又方程可变形为
的取值范围,又方程可变形为 ,因此求
,因此求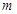 的取值范围,就相当于求函数
的取值范围,就相当于求函数
 的值域,用换元法(设
的值域,用换元法(设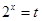 ),再借助于函数
),再借助于函数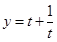 的单调性就可求出.
的单调性就可求出.试题解析:(1)
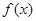 为“局部奇函数”等价于关于
为“局部奇函数”等价于关于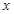 的方程
的方程 有解.
有解.即
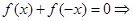
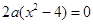 (3分)
(3分)有解
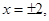
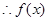 为“局部奇函数”.(5分)
为“局部奇函数”.(5分)(2)当
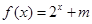 时,
时, 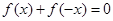 可转化为
可转化为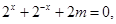 (8分)
(8分)因为
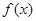 的定义域为
的定义域为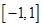 ,所以方程
,所以方程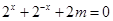 在
在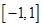 上有解,令
上有解,令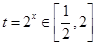 ,(9分)
,(9分)则

因为
 在
在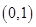 上递减,在
上递减,在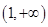 上递增,
上递增,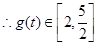 (11分)
(11分) (12分)
(12分)即
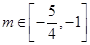 (14分)
(14分)
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 表示成分数幂的形式。
表示成分数幂的形式。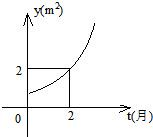
 上的偶函数,
上的偶函数, 满足
满足 ,都有
,都有 ,且当
,且当 时,
时, .若函数
.若函数 在
在 上有三个零点,则
上有三个零点,则 的取值范围是 .
的取值范围是 . 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组 所确定的平面区域在
所确定的平面区域在 内的面积为 ( )
内的面积为 ( )



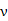 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度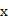 (单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当
(单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当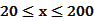 时,车流速度
时,车流速度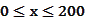 时,求函数
时,求函数 的表达式;
的表达式;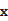 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)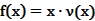 可以达到最大?并求出最大值。(精确到1辆/小时)
可以达到最大?并求出最大值。(精确到1辆/小时)