Question

已知定义在R上的函数f（x）满足：f（x+1）=，当x∈（0，1]时，f（x）=2^x，则f（log₂9）等于________．

Answer 1

分析：根据题意，算出f（x+2）=f（x），得f（x）是最小正周期为2的周期函数．从而算出f（log₂9）=f（log₂）．由x∈（0，1]时f（x）=2^x，结合f（x+1）f（x）=1算出f（log₂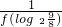）==，即可得到所求的函数值．
解答：∵f（x+1）=，
∴f（x+2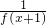）===f（x），可得f（x）是最小正周期为2的周期函数
∵8＜9＜16，2＞1
∴log₂8＜log₂9＜log₂16，即log₂9∈（3，4）
因此f（log₂9）=f（log₂9-2）=f（log₂）
∵f（log₂）==
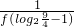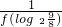
而f（log₂）==，
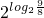∴f（log₂9）=f（log₂）==
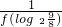故答案为：
点评：本题给出函数满足的条件，求特殊自变量对应的函数值．着重考查了函数的周期性及其证明、对数的运算法则和函数性质的理解等知识，属于中档题．