Question

（07年天津卷理）(14分)

    在数列中N其中.

    (I)求数列的通项公式；

    (II)求数列的前项和；

    (III)证明存在N使得对任意N均成立.

Answer 1

解析：(I)解法一：，

    ，

    .

    由此可猜想出数列的通项公式为.

    以下用数学归纳法证明.

    (1)当时等式成立.

    (2)假设当时等式成立，即

那么，

这就是说，当时等式也成立.根据(1)和(2)可知，等式对任何N都成立.

解法二：由N可得

    所以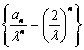为等数列，其公差为1，首项为0.故

所以数列的通项公式为

(II)设                 ①

             ②

    当时，①式减去②式，得

   

   

    这时数列的前项和

    当 时，这时数列的前项和

(III)证明：通过分析，推测数列的第一项最大.下面证明： ③

    由知要使③式成立，只要因为

   

              

    所以③式成立. 因此，存在使得对任意N均成立.

【考点】本小题以数列的递推关系式为载体，主要考查等比数列的前项和公式、数列求和、不等式的证明等基础知识与基本方法，考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.