题目内容
已知数列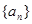 满足
满足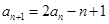 (
(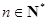 ).
).
(1)若数列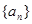 是等差数列,求数列
是等差数列,求数列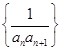 的前
的前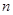 项和
项和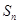 ;
;
(2)证明:数列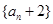 不可能是等比数列.
不可能是等比数列.
(1)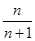 (2)详见解析.
(2)详见解析.
解析试题分析:(1)设等差数列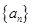 的公差为
的公差为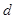 ,将
,将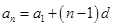 代入
代入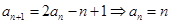
所以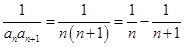 ,于是可以用裂项法求数列
,于是可以用裂项法求数列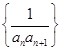 的前
的前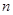 项和
项和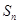 ;
;
(2)用反证法,假设数列 是等比数列,则
是等比数列,则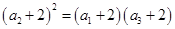 ,结合题设中的递推公式解出
,结合题设中的递推公式解出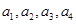 导出矛盾.
导出矛盾.
解:(1)解法一:∵ 数列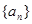 是等差数列,设其首项为
是等差数列,设其首项为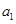 ,公差为
,公差为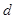 ,则
,则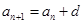
∴ 由已知可得: 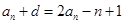 即
即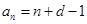
又 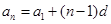
∴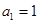 ,
,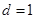 可得:
可得: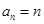
∴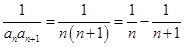
故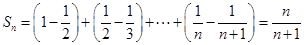 6分
6分
解法二:由已知,得: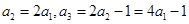
所以由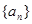 是等差数列,得:
是等差数列,得: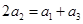
即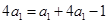 可得
可得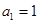 ,易得公差
,易得公差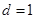

经检验符合(以下同解法一)
证明:(2)假设数列 是等比数列,则
是等比数列,则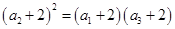
即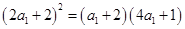
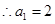 ,
,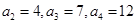
于是数列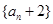 的前4项为:4,6,9,14,它显然不是等比数列
的前4项为:4,6,9,14,它显然不是等比数列
故数列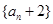 不是等比数列 12分
不是等比数列 12分
考点:1、等差数列与等比数列;2、特殊数列求和.

练习册系列答案
相关题目
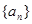 的前
的前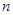 项和为
项和为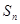 ,
,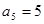 ,
,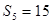 ,
,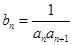 ,求数列
,求数列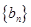 的前100项和.
的前100项和. 中,
中,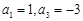 .
.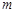 项和
项和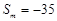 ,求
,求 满足:
满足: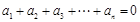 且
且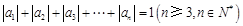 ,则称数列
,则称数列 阶“归化数列”.
阶“归化数列”.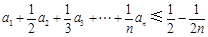 .
.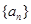 是等差数列,
是等差数列,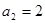 ,前四项和
,前四项和 。
。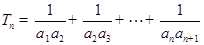 ,计算
,计算 。
。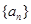 的各项均为正数,记
的各项均为正数,记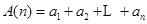 ,
,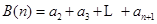 ,
,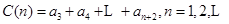 .
.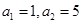 ,且对任意
,且对任意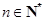 ,三个数
,三个数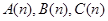 组成等差数列,求数列
组成等差数列,求数列 的等比数列的充分必要条件是:对任意
的等比数列的充分必要条件是:对任意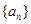 中,
中,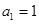 ,对于任意
,对于任意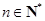 ,都有
,都有 ,
,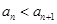 . 设
. 设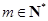 , 记使得
, 记使得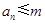 成立的
成立的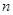 的最大值为
的最大值为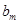 .
.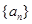 为1,3,5,7,
为1,3,5,7,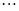 ,写出
,写出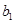 ,
,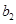 ,
,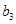 的值;
的值;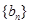 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列 ,
,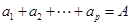 ,求
,求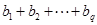 的值.(用
的值.(用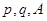 表示)
表示)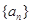 的前n项和为
的前n项和为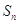 ,存在常数A,B,C,使得
,存在常数A,B,C,使得 对任意正整数n都成立.
对任意正整数n都成立.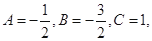 设
设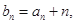 数列
数列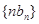 的前n项和为
的前n项和为 ,求
,求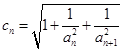 数列
数列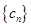 的前2014项和为P,求不超过P的最大整数的值.
的前2014项和为P,求不超过P的最大整数的值.