Question

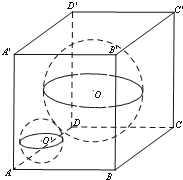如图，球O是棱长为2的正方体的内切球（与正方体的各个面均相切），现在要在正方体内放置一个小球O′，使球O′与正方体的三个面及球O均相切，则球O′的半径为

 

．

Answer 1

分析：作出对应图象的轴截面图，利用相应的关系 建立条件关系，即可求球的半径．

解答：解：∵正方体的棱长为2，
∴正方体的内切球的半径R=1，正方体的体对角线为2

3

，
设小球球O′的半径为r，
作出对应的轴截面图如图：
则OE∥C'C，
且O'A=

3

r，O'O=r+1
∴O'A+O'O=OA=

3

，
即

3

r+r+1=

3

，
（

3

+1）r=

3

-1，
r=

3 -1

3 +1

=2-

3

．
故答案为：2-

3

．

点评：本题主要考查空间正方体与球的内切问题，根据条件建立球半径之间的关系是解决本题的关键．