题目内容
（本小题满分12分）
已知椭圆C的中心在原点，焦点在
轴上，它的一个顶点恰好是抛物线
的焦点，离心率等于
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过椭圆C的右焦点作直线
交椭圆C于A，B两点，交
轴于M点，若
，求证：
为定值，点F即是椭圆C的右焦点。
解：
（1）设椭圆
的方程为
，
则由题意知
，
，
， ————3分
椭圆的方程为
——————4分
（2）证明：设
点的坐标分别为
，
易知
点的坐标为（2，0）。————5分
由
有，
， ——————6分
由
有，
， ——————7分
则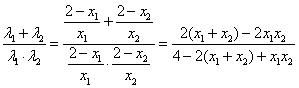
，（※） ——————9分
设直线
代入椭圆方程，
有
由韦达定理
代入（※） ——————11分
有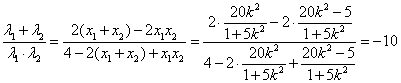
。 ———12分
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
