题目内容
设函数 ,集合M={x|f(x)=0}={x1,x2,…,x19}⊆N*,设c1≥c2≥…≥c10,则c1-c10=
,集合M={x|f(x)=0}={x1,x2,…,x19}⊆N*,设c1≥c2≥…≥c10,则c1-c10=
- A.83
- B.85
- C.79
- D.81
D
分析:根据已知M={x|f(x)=0}={x1,x2,…,x19}⊆N*,可得函数 ,共有19个零点,结合韦达定理可得xn=n,1≤n≤19,n∈N*,
,共有19个零点,结合韦达定理可得xn=n,1≤n≤19,n∈N*,
结合c1≥c2≥…≥c10,求出c1,c10,代入c1-c10可得答案.
解答:∵函数 ,
,
∵M={x|f(x)=0}={x1,x2,…,x19}⊆N*,
令0<x1<x2<…<x19,
则由韦达定理可得
x1+x19=x2+x18=…=x10+x10=20
则x19<20
故xn=n,1≤n≤19,n∈N*,
∴x1•x19<x2•x18<…<x10•x10,
又∵c1≥c2≥…≥c10,
∴c10=x1•x19=19,c1=x10•x10=100
即c1-c10=100-19=81
故选D
点评:本题考查的知识点是一元二次方程的根的分布与系数的关系(韦达定理),函数的零点与方程的根的关系,其中根据已知得到xn=n,1≤n≤19,n∈N*,是解答的关键.
分析:根据已知M={x|f(x)=0}={x1,x2,…,x19}⊆N*,可得函数
 ,共有19个零点,结合韦达定理可得xn=n,1≤n≤19,n∈N*,
,共有19个零点,结合韦达定理可得xn=n,1≤n≤19,n∈N*,结合c1≥c2≥…≥c10,求出c1,c10,代入c1-c10可得答案.
解答:∵函数
 ,
,∵M={x|f(x)=0}={x1,x2,…,x19}⊆N*,
令0<x1<x2<…<x19,
则由韦达定理可得
x1+x19=x2+x18=…=x10+x10=20
则x19<20
故xn=n,1≤n≤19,n∈N*,
∴x1•x19<x2•x18<…<x10•x10,
又∵c1≥c2≥…≥c10,
∴c10=x1•x19=19,c1=x10•x10=100
即c1-c10=100-19=81
故选D
点评:本题考查的知识点是一元二次方程的根的分布与系数的关系(韦达定理),函数的零点与方程的根的关系,其中根据已知得到xn=n,1≤n≤19,n∈N*,是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( )
,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( ) ,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( )
,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( )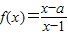 ,集合M={x|f(x)<0},P={x|f′(x)>0},若M⊆P,则实数a的取值范围是 .
,集合M={x|f(x)<0},P={x|f′(x)>0},若M⊆P,则实数a的取值范围是 .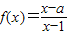 ,集合M={x|f(x)<0},P={x|f'(x)>0},若M?P,则实数a的取值范围是( )
,集合M={x|f(x)<0},P={x|f'(x)>0},若M?P,则实数a的取值范围是( ) ,集合M={x|f(x)<0},P={x|f'(x)>0},若M?P,则实数a的取值范围是( )
,集合M={x|f(x)<0},P={x|f'(x)>0},若M?P,则实数a的取值范围是( )