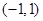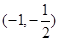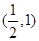题目内容
函数f(x)=x2+x-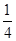 .
.
(I)若定义域为[0,3],求f(x)的值域;
(II)若f(x)的值域为[-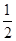 ,
,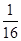 ],且定义域为[a,b],求b-a的最大值.
],且定义域为[a,b],求b-a的最大值.
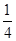 .
.(I)若定义域为[0,3],求f(x)的值域;
(II)若f(x)的值域为[-
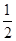 ,
,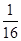 ],且定义域为[a,b],求b-a的最大值.
],且定义域为[a,b],求b-a的最大值. (I) [-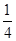 ,
,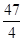 ] (II)
] (II)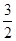
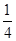 ,
,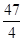 ] (II)
] (II)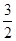
试题分析:解:∵f(x)=(x+
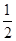 )2-
)2-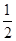 ,∴对称轴为x=-
,∴对称轴为x=-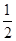 .
.(1)∵3≥x≥0>-
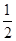 ,
,∴f(x)的值域为[f(0),f(3)],即[-
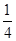 ,
,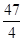 ];
];(2)∵x=-
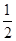 时,f(x)=-
时,f(x)=-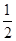 是f(x)的最小值,
是f(x)的最小值,∴x=-
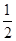 ∈[a,b],令x2+x-
∈[a,b],令x2+x-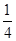 =
=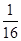 ,
,得x1=-
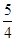 ,x2=
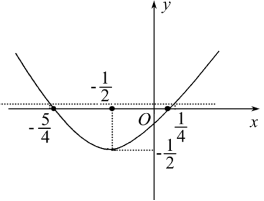
,x2=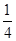 ,根据f(x)的图象知b-a的最大值是
,根据f(x)的图象知b-a的最大值是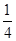 -(-
-(-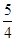 )=
)=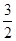 .
.
点评:求函数的值域,只要确定函数的最小值和最大值即可,最小值与最大值之间的范围就是值域。

练习册系列答案
相关题目
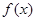 的定义域为
的定义域为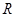 ,则
,则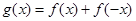 一定是偶函数;
一定是偶函数;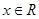 都有
都有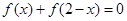 ,则函数
,则函数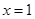 对称;
对称;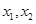 是函数
是函数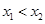 时,
时,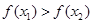 ,则
,则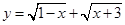 的最大值和最小值分别为
的最大值和最小值分别为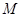 和
和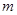 ,则
,则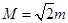 ;
;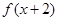 也为奇函数,则
也为奇函数,则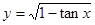 的定义域是__________。
的定义域是__________。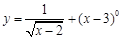 的定义域为
的定义域为 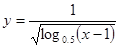 的定义域是 .
的定义域是 .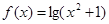 的值域为
的值域为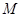 ,函数
,函数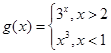 的定义域为
的定义域为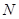 ,则
,则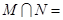
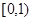
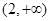

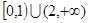
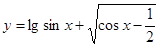 的定义域为 .
的定义域为 . 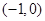 ,则函数
,则函数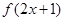 的定义域( )
的定义域( )