题目内容
7.已知数列{a }满足a=$\frac{4}{3}$,an+1-1=an2-an (n∈N*),则m=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2017}}$的整数部分是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先判断数列{an}是单调递增数列,再根据数列的递推公式利用裂项求和即可得到m=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2017}}$=3-$\frac{1}{{a}_{2018}-1}$,再根据数列的单调性判断出a2018>2,问题得以解决
解答 解:∵a=$\frac{4}{3}$,an+1-1=an2-an (n∈N*),
∴an+1-an=an2+1>0,
∴an+1>an,
∴数列{an}是单调递增数列,
由an+1-1=an2-an=an(an-1),
∴$\frac{1}{{a}_{n+1}-1}$=$\frac{1}{{a}_{n}({a}_{n}-1)}$=$\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n}}$,
∴$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n+1}-1}$,
∴m=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2017}}$=($\frac{1}{{a}_{1}-1}$-$\frac{1}{{a}_{2}-1}$)+($\frac{1}{{a}_{2}-1}$-$\frac{1}{{a}_{3}-1}$)+…+($\frac{1}{{a}_{2017}-1}$-$\frac{1}{{a}_{2018}-1}$)=$\frac{1}{{a}_{1}-1}$-$\frac{1}{{a}_{2018}-1}$=3-$\frac{1}{{a}_{2018}-1}$,
由a=$\frac{4}{3}$>1,则an+1-an=(an-1)2>0,
∴a2=1+$\frac{4}{9}$,a3=1+$\frac{52}{81}$,a4=1+$\frac{6916}{6561}$>2,
…,
a2018>2,
∴0<$\frac{1}{{a}_{2018}-1}$<1,
∴2<m<3,
∴整数部分是2,
故选:B
点评 本题考查了数列与函数的特征,以及数列的递推关系裂项求和,考查了学生的运算能力和转化能力,属于中档题

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | $\sqrt{29}$-$\sqrt{13}$ | B. | 5+$\sqrt{13}$ | C. | 2$\sqrt{7}$+$\sqrt{13}$ | D. | $\sqrt{29}$+$\sqrt{13}$ |
| A. | 50π | B. | 100π | C. | 200π | D. | $\frac{{125\sqrt{2}π}}{3}$ |
| A. | {0,1} | B. | {0,2} | C. | {1,3} | D. | {2,3} |
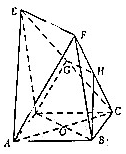 如图,在多面体ABCDEF中,底面ABCD是边长为1的正方形,四边形BDEF是矩形,且BF=2,CF=$\sqrt{5}$,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为1的正方形,四边形BDEF是矩形,且BF=2,CF=$\sqrt{5}$,G和H分别是CE和CF的中点.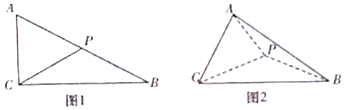 如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得AB=$\sqrt{10}$.
如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得AB=$\sqrt{10}$.