题目内容
已知 为
为 奇函数。
奇函数。
(1)求 的值;
的值;
(2)若 且
且 ,求
,求 的值;
的值;
(3)若对于任意的 ,函数
,函数 ,
, 满足
满足 ,则称在
,则称在 上
上 与
与 具有“H类关系”。问函
具有“H类关系”。问函 数
数 与函
与函 数
数 在
在 上是否具有“H类关系”,并结合函数单调性的定义证明你的结论。
上是否具有“H类关系”,并结合函数单调性的定义证明你的结论。
解: (1)a=0 ,b=2 ,c=1
(2)T(8)+T(-8)=20 ,T (8)=18
(8)=18
(3)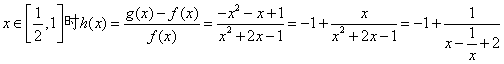
是减函数(证明略 )
)

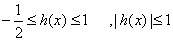 即
即 ,f(x)与g(x)具有“H类关系”
,f(x)与g(x)具有“H类关系”

练习册系列答案
相关题目
题目内容
已知 为
为 奇函数。
奇函数。
(1)求 的值;
的值;
(2)若 且
且 ,求
,求 的值;
的值;
(3)若对于任意的 ,函数
,函数 ,
, 满足
满足 ,则称在
,则称在 上
上 与
与 具有“H类关系”。问函
具有“H类关系”。问函 数
数 与函
与函 数
数 在
在 上是否具有“H类关系”,并结合函数单调性的定义证明你的结论。
上是否具有“H类关系”,并结合函数单调性的定义证明你的结论。
解: (1)a=0 ,b=2 ,c=1
(2)T(8)+T(-8)=20 ,T (8)=18
(8)=18
(3)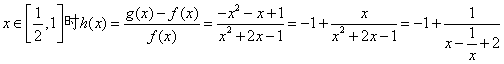
是减函数(证明略 )
)

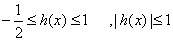 即
即 ,f(x)与g(x)具有“H类关系”
,f(x)与g(x)具有“H类关系”
