题目内容
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 的准线,
的准线,![]() 轴,
轴,![]() 轴,
轴,![]() 、
、![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,交
两点,交![]() 于
于![]() 、
、![]() 两点,已知
两点,已知![]() 的面积是
的面积是![]() 的2倍,则
的2倍,则![]() 中点
中点![]() 到
到![]() 轴的距离的最小值为( )
轴的距离的最小值为( )
A.![]() B.1C.
B.1C.![]() D.2
D.2
【答案】B
【解析】
由题可知![]() ,准线方程为
,准线方程为![]() ,设
,设![]() ,可得
,可得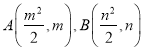 ,分类讨论,当
,分类讨论,当![]() 轴时,可得中点到
轴时,可得中点到![]() 的距离为
的距离为![]() ;当
;当![]() 不垂直于
不垂直于![]() 轴时,求出直线
轴时,求出直线![]() 的方程,利用点到直线的距离公式以及弦长公式求出
的方程,利用点到直线的距离公式以及弦长公式求出![]() 的面积,在求出
的面积,在求出![]() 的面积,根据两个三角形的面积关系可得
的面积,根据两个三角形的面积关系可得![]() ,
,![]() 中点
中点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,利用基本不等式即可求解.
,利用基本不等式即可求解.
由题可知![]() ,准线方程为
,准线方程为![]() ,如图:
,如图:
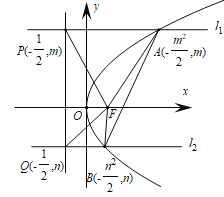
设![]() ,则
,则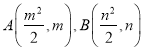 ,
,
当![]() 轴时,其中点到
轴时,其中点到![]() 的距离为
的距离为![]() .
.
当![]() 不垂直于
不垂直于![]() 轴时,直线
轴时,直线![]() 的方程为:
的方程为:![]() ,
,
设![]() 点到直线
点到直线![]() 的距离为
的距离为![]() ,则
,则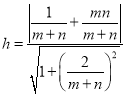 ,
,
而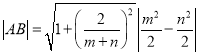 ,
,
所以有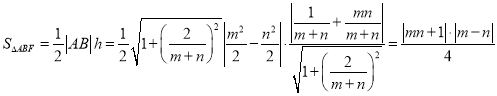 ,
,
又![]() ,
,
因为已知![]() 的面积是
的面积是![]() 的2倍,
的2倍,
即![]() ,化简可得
,化简可得![]() (不合题意舍去)或
(不合题意舍去)或![]() ,
,
![]() 中点
中点![]() 到
到![]() 轴的距离
轴的距离![]() (
(![]() ,不能取等号)
,不能取等号)
综上,![]() 中点
中点![]() 到
到![]() 轴的距离最小值为1.
轴的距离最小值为1.
故选:B

练习册系列答案
相关题目
【题目】已知函数![]() 的定义域
的定义域![]() ,部分对应值如表,
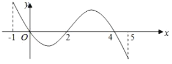
,部分对应值如表,![]() 的导函数
的导函数![]() 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数![]() 的结论正确的是( )
的结论正确的是( )
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
A.函数![]() 的极大值点有2个
的极大值点有2个
B.函数![]() 在
在![]() 上是减函数
上是减函数
C.若![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最大值为4
的最大值为4
D.当![]() 时,函数
时,函数![]() 有4个零点
有4个零点