题目内容
已知等差数列
的公差和首项都不等于0，且
，
，
成等比数列，则
( )
| A．2 | B．3 | C．5 | D．7 |
A
解析试题分析：设公差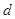为
，因为，，成等比数列，所以
，即
，解得
，所以
.
考点：1、等差数列的通项公式；2、等比数列的性质.
练习册系列答案
相关题目
已知等比数列
的公比
,且
,
,48成等差数列,则的前8项和为( )
| A．127 | B．255 | C．511 | D．1023 |
已知等比数列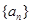
，且
，则
的值为（ ）
A． | B． | C． | D． |
数列
中，若
，则该数列的通项
（ ）
A． | B． | C． | D． |
等比数列
的各项均为正数，且
，则
（ ）
| A．12 | B．10 | C． | D． |
数列
等比数列，
，
，则数列
的前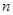
项的和为（ ）
A． | B． | C． | D． |
已知数列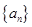
是各项均为正数的等比数列，
=1，
=4，则
=（ ）
| A．20 | B．32 | C．80 | D． |
已知等比数列{an}，且
，则
的值为（ ）
| A．π2 | B．4 | C．π | D．-9π |
等比数列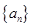
中，
，
=4，函数
，则
（ ）
A． | B． | C． | D． |