题目内容
已知数列{an}满足条件:a1=t,an+1=2an+1.(I)判断数列{an+1}是否为等比数列;
(Ⅱ)若
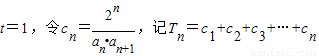 .
.证明:
(i)
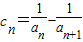 ;
;(ii)Tn<1.
【答案】分析:(I)由题意可得,an+1+1=2an+2=2(an+1),a1+1=t+1,结合等比数列的定义,考虑t的取值,即可判断
(II)当t=1时,由(I)知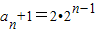 ,则可求
,则可求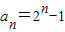 ,代入求出cn,然后利用裂项即可求和,可证
,代入求出cn,然后利用裂项即可求和,可证
解答:解(I)由题意可得,an+1+1=2an+2=2(an+1)
∵a1+1=t+1
∴当t=-1时,数列{an+1}不是等比数列
当t≠-1时,数列{an+1}是以t+1为首项,以2为公比的等比数列;
(II)当t=1时,由(I)知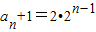
∴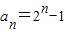
∴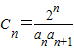 =
=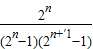 =
=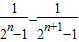 =
=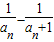
∴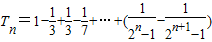
=1-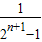 <1
<1
点评:本题主要考查了 等比数列的 定义及等比数列的通项公式的应用,数列的裂项求和方法的应用.
(II)当t=1时,由(I)知
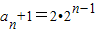 ,则可求
,则可求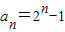 ,代入求出cn,然后利用裂项即可求和,可证
,代入求出cn,然后利用裂项即可求和,可证解答:解(I)由题意可得,an+1+1=2an+2=2(an+1)
∵a1+1=t+1
∴当t=-1时,数列{an+1}不是等比数列
当t≠-1时,数列{an+1}是以t+1为首项,以2为公比的等比数列;
(II)当t=1时,由(I)知
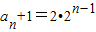
∴
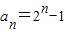
∴
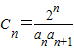 =
=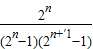 =
=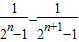 =
=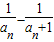
∴
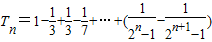
=1-
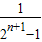 <1
<1点评:本题主要考查了 等比数列的 定义及等比数列的通项公式的应用,数列的裂项求和方法的应用.

练习册系列答案
相关题目