题目内容
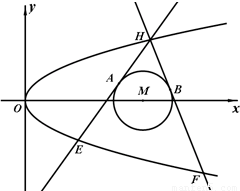
如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x,y)(y≥1)作两条直线与⊙M相切于A、两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为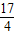 .
.(Ⅰ)求抛物线C的方程;
(Ⅱ)当∠AHB的角平分线垂直x轴时,求直线EF的斜率;
(Ⅲ)若直线AB在y轴上的截距为t,求t的最小值.
【答案】分析:(Ⅰ)利用点M到抛物线准线的距离为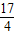 ,可得
,可得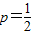 ,从而可求抛物线C的方程;
,从而可求抛物线C的方程;
(Ⅱ)法一:根据当∠AHB的角平分线垂直x轴时,点H(4,2),可得kHE=-kHF,设E(x1,y1),F(x2,y2),可得y1+y2=-2yH=-4,从而可求直线EF的斜率;
法二:求得直线HA的方程为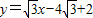 ,与抛物线方程联立,求出E,F的坐标,从而可求直线EF的斜率;
,与抛物线方程联立,求出E,F的坐标,从而可求直线EF的斜率;
(Ⅲ)法一:设A(x1,y1),B(x2,y2),求出直线HA的方程,直线HB的方程,从而可得直线AB的方程,令x=0,可得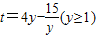 ,再利用导数法,即可求得t的最小值.
,再利用导数法,即可求得t的最小值.
法二:求以H为圆心,HA为半径的圆方程,⊙M方程,两方程相减,可得直线AB的方程,当x=0时,直线AB在y轴上的截距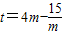 (m≥1),再利用导数法,即可求得t的最小值.
(m≥1),再利用导数法,即可求得t的最小值.
解答:解:(Ⅰ)∵点M到抛物线准线的距离为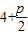 =
=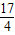 ,
,
∴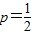 ,∴抛物线C的方程为y2=x.(2分)
,∴抛物线C的方程为y2=x.(2分)
(Ⅱ)法一:∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴kHE=-kHF,
设E(x1,y1),F(x2,y2),∴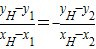 ,∴
,∴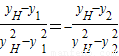 ,
,
∴y1+y2=-2yH=-4.(5分)
∴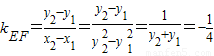 .(7分)
.(7分)
法二:∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴∠AHB=60°,可得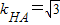 ,
,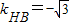 ,
,
∴直线HA的方程为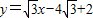 ,
,
联立方程组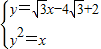 ,得
,得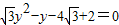 ,
,
∵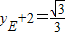
∴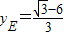 ,
,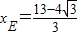 .(5分)
.(5分)
同理可得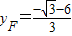 ,
,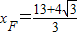 ,∴
,∴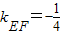 .(7分)
.(7分)
(Ⅲ)法一:设A(x1,y1),B(x2,y2),∵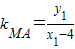 ,∴
,∴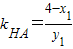 ,
,
∴直线HA的方程为(4-x1)x-y1y+4x1-15=0,
同理,直线HB的方程为(4-x2)x-y2y+4x2-15=0,
∴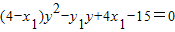 ,
,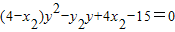 ,(9分)
,(9分)
∴直线AB的方程为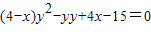 ,
,
令x=0,可得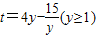 ,
,
∵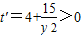 ,∴t关于y的函数在[1,+∞)上单调递增,
,∴t关于y的函数在[1,+∞)上单调递增,
∴当y=1时,tmin=-11.(12分)
法二:设点H(m2,m)(m≥1),HM2=m4-7m2+16,HA2=m4-7m2+15.
以H为圆心,HA为半径的圆方程为(x-m2)2+(y-m)2=m4-7m2+15,①
⊙M方程:(x-4)2+y2=1.②
①-②得:直线AB的方程为(2x-m2-4)(4-m2)-(2y-m)m=m4-7m2+14.(9分)
当x=0时,直线AB在y轴上的截距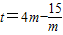 (m≥1),
(m≥1),
∵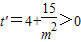 ,∴t关于m的函数在[1,+∞)上单调递增,
,∴t关于m的函数在[1,+∞)上单调递增,
∴当m=1时,tmin=-11.(12分)
点评:本题以抛物线与圆的方程为载体,考查抛物线的标准方程,考查直线方程,同时考查利用导数法解决函数的最值问题,综合性较强.
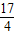 ,可得
,可得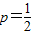 ,从而可求抛物线C的方程;
,从而可求抛物线C的方程;(Ⅱ)法一:根据当∠AHB的角平分线垂直x轴时,点H(4,2),可得kHE=-kHF,设E(x1,y1),F(x2,y2),可得y1+y2=-2yH=-4,从而可求直线EF的斜率;
法二:求得直线HA的方程为
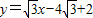 ,与抛物线方程联立,求出E,F的坐标,从而可求直线EF的斜率;
,与抛物线方程联立,求出E,F的坐标,从而可求直线EF的斜率;(Ⅲ)法一:设A(x1,y1),B(x2,y2),求出直线HA的方程,直线HB的方程,从而可得直线AB的方程,令x=0,可得
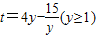 ,再利用导数法,即可求得t的最小值.
,再利用导数法,即可求得t的最小值.法二:求以H为圆心,HA为半径的圆方程,⊙M方程,两方程相减,可得直线AB的方程,当x=0时,直线AB在y轴上的截距
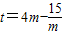 (m≥1),再利用导数法,即可求得t的最小值.
(m≥1),再利用导数法,即可求得t的最小值.解答:解:(Ⅰ)∵点M到抛物线准线的距离为
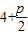 =
=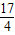 ,
,∴
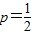 ,∴抛物线C的方程为y2=x.(2分)
,∴抛物线C的方程为y2=x.(2分)(Ⅱ)法一:∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴kHE=-kHF,
设E(x1,y1),F(x2,y2),∴
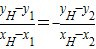 ,∴
,∴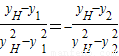 ,
,∴y1+y2=-2yH=-4.(5分)
∴
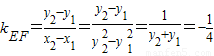 .(7分)
.(7分)法二:∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴∠AHB=60°,可得
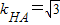 ,
,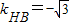 ,
,∴直线HA的方程为
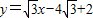 ,
,联立方程组
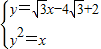 ,得
,得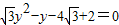 ,
,∵
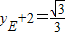
∴
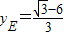 ,
,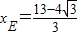 .(5分)
.(5分)同理可得
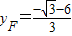 ,
,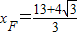 ,∴
,∴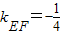 .(7分)
.(7分)(Ⅲ)法一:设A(x1,y1),B(x2,y2),∵
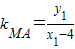 ,∴
,∴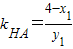 ,
,∴直线HA的方程为(4-x1)x-y1y+4x1-15=0,
同理,直线HB的方程为(4-x2)x-y2y+4x2-15=0,
∴
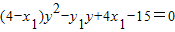 ,
,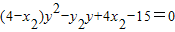 ,(9分)
,(9分)∴直线AB的方程为
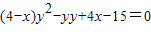 ,
,令x=0,可得
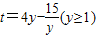 ,
,∵
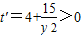 ,∴t关于y的函数在[1,+∞)上单调递增,
,∴t关于y的函数在[1,+∞)上单调递增,∴当y=1时,tmin=-11.(12分)
法二:设点H(m2,m)(m≥1),HM2=m4-7m2+16,HA2=m4-7m2+15.
以H为圆心,HA为半径的圆方程为(x-m2)2+(y-m)2=m4-7m2+15,①
⊙M方程:(x-4)2+y2=1.②
①-②得:直线AB的方程为(2x-m2-4)(4-m2)-(2y-m)m=m4-7m2+14.(9分)
当x=0时,直线AB在y轴上的截距
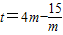 (m≥1),
(m≥1),∵
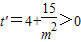 ,∴t关于m的函数在[1,+∞)上单调递增,
,∴t关于m的函数在[1,+∞)上单调递增,∴当m=1时,tmin=-11.(12分)
点评:本题以抛物线与圆的方程为载体,考查抛物线的标准方程,考查直线方程,同时考查利用导数法解决函数的最值问题,综合性较强.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点). 如图,已知抛物线C:x2=2py(p>0)与圆O:x2+y2=8相交于A、B两点,且
如图,已知抛物线C:x2=2py(p>0)与圆O:x2+y2=8相交于A、B两点,且 (2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.
(2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ. (2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.
(2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.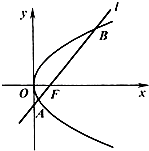 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.