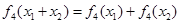题目内容
已知如下等式:
3-4=
(32-42),
32-3×4+42=
(33+43),
33-32×4+3×42-43=
(34-44),
34-33×4+32×42-3×43+44=
(35+45),…
则由上述等式可归纳得到3n-3n-1×4+3n-2×42-…+(-1)n4n=
[3n+1-(-4)n+1](n∈N*)
[3n+1-(-4)n+1](n∈N*)(n∈N*).
3-4=
| 1 |
| 7 |
32-3×4+42=
| 1 |
| 7 |
33-32×4+3×42-43=
| 1 |
| 7 |
34-33×4+32×42-3×43+44=
| 1 |
| 7 |
则由上述等式可归纳得到3n-3n-1×4+3n-2×42-…+(-1)n4n=
| 1 |
| 7 |
| 1 |
| 7 |
分析:本题考查的知识点是归纳推理,我们可以根据已知条件中的等式,分析等式两边的系数及指数部分与式子编号之间的关系,归纳出第n(n∈N*)个等式.
解答:解:根据各个式子右端
(32-42),
(33+43),
(34-44)…,
由归纳推理,可得原式=
[3n+1-(-4)n+1](n∈N*).
故答案为:
[3n+1-(-4)n+1](n∈N*)
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
由归纳推理,可得原式=
| 1 |
| 7 |
故答案为:
| 1 |
| 7 |
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
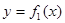 (2)
(2)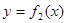 (3)
(3)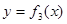 (4)
(4)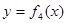 的图象如下:
的图象如下:

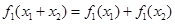 B.
B. 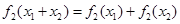
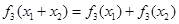 D.
D.