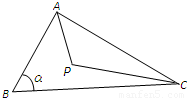
题目内容
点P在△ABC内，并且
+
=6
，设△ABC的面积是△PBC的面积的m倍，那么m=（ ）
| PB |
| PC |
| AP |
| A．1 | B．
| C．4 | D．2 |
∵点P在三角形ABC内，
∴M＞1．记
+
=
，交BC与E．
又
+
=6
，
所以
，
共线，
所以点E是BC的中点．且E点平分PD．
所以
=
，
△ABC与△PBC同底，
它们的高之比=
=
m=
故选B
∴M＞1．记
| PB |
| PC |
| PD |
又
| PB |
| PC |
| AP |
所以
| AP |
| PD |
所以点E是BC的中点．且E点平分PD．
所以
| ||
|
| 1 |
| 3 |
△ABC与△PBC同底，
它们的高之比=
| ||
|
| 4 |
| 3 |
m=
| 4 |
| 3 |
故选B
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
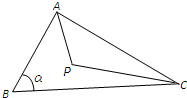如图，点P在△ABC内，AB=CP=2，BC=3，∠P+∠B=π，记∠B=α．
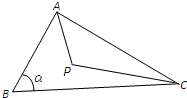如图，点P在△ABC内，AB=CP=2，BC=3，∠P+∠B=π，记∠B=α．
