题目内容
设函数f(x)=xsinx(x∈R),
(Ⅰ)证明f(x+2kπ)-f(x)=2kπsinx,其中k为整数;
(Ⅱ)设x0为f(x)的一个极值点,证明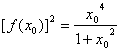 ;
;
(Ⅲ)设f(x)在(0,+∞)内的全部极值点按从小到大的顺序排列a1,a2,…,an,…,证明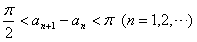 。
。
| (Ⅰ)证明:由函数f (x)的定义,对任意整数k, 有 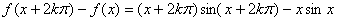 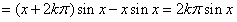 ; ; |
|
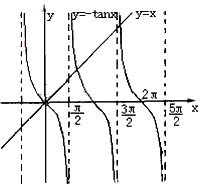
(Ⅱ)证明:函数f(x)在定义域R上可导,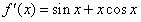 , ① , ① 令f′(x)=0,得sinx+xcosx=0, 显然,对于满足上述方程的x有cosx≠0, 上述方程化简为x=-tanx, 如图所示,此方程一定有解, f(x)的极值点x0一定满足 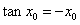 , ,由 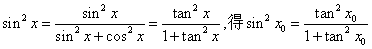 , ,因此, 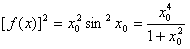 ; ; |
 |
| (Ⅲ)证明:设x0>0是f′(x)=0的任意正实根, 即 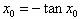 , ,则存在一个非负整数k,使 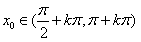 , ,即x0在第二或第四象限内, 由①式, 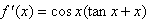 在第二象限或第四象限中的符号 在第二象限或第四象限中的符号可列表如下: 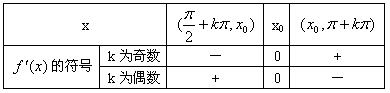 所以满足 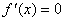 的正根x0都为f(x)的极值点, 的正根x0都为f(x)的极值点,由题设条件, 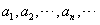 为方程x=-tanx的全部正实根且满足 为方程x=-tanx的全部正实根且满足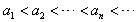 , ,那么对于n=1,2,…,   , ② , ② 由于 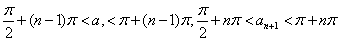 , ,则 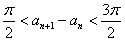 , ,由于  , ,由②式知 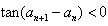 , ,由此可知 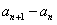 必在第二象限,即 必在第二象限,即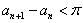 ; ; 综上, 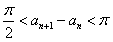 。 。 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
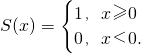 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).