题目内容
关于函数f(x)=sinx+cosx下列命题正确的是( )
| A、函数f(x)最大值为2 | ||
B、函数f(x)的一条对称轴为x=
| ||
C、函数f(x)的图象向左平移
| ||
| D、函数y=|f(x)|的周期为2π |
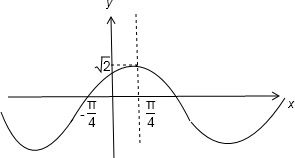
分析:把f(x)利用两角和的正弦函数公式化成一个三角函数,图象如图,根据函数的图象得到函数的最大值,对称轴,平移后图象的奇偶性,和函数的周期,得到正确答案.
解答:解:f(x)=sinx+cosx=
(
sinx+
cosx)=
(sinxcos
+cosxsin
)=
sin(x+
)
根据-1≤sin(x+
)≤1得到-
≤
sin(x+
)≤
,所以函数f(x)的最大值为
,A错;
根据图象可知函数f(x)的一条对称轴为x=
,B正确;
函数f(x)的图象向左平移
个单位后对应的函数是偶函数,C错;
函数y=|f(x)|的图象即为把图中的x轴以下的部分对称到x轴上面,函数y的周期应为kπ+
k∈Z,所以2π不是函数的周期,D错.
故选B.
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
根据-1≤sin(x+
| π |
| 4 |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
| 2 |
根据图象可知函数f(x)的一条对称轴为x=
| π |
| 4 |
函数f(x)的图象向左平移
| π |
| 4 |
函数y=|f(x)|的图象即为把图中的x轴以下的部分对称到x轴上面,函数y的周期应为kπ+
| 3π |
| 4 |
故选B.

点评:考查学生利用数形结合的思想解决数学问题,要求学生灵活两角和与差的正弦函数公式化简求值,会求函数的周期及掌握函数的平移的规律,会求函数的周期.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 已知二次函数f(x)=ax2+bx+c,直线l1:y=-t2+8t(其中0≤t≤2,t为常数);l2:x=2.若直线l1、l2与函数f(x)的图象以及l1、y轴所围成的封闭图形如阴影所示.
已知二次函数f(x)=ax2+bx+c,直线l1:y=-t2+8t(其中0≤t≤2,t为常数);l2:x=2.若直线l1、l2与函数f(x)的图象以及l1、y轴所围成的封闭图形如阴影所示. 已知二次函数f(x)=ax2+bx+c,直线l1:x=2,l2:y=-t2+8t(其中0≤t≤2.t为常数);若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.
已知二次函数f(x)=ax2+bx+c,直线l1:x=2,l2:y=-t2+8t(其中0≤t≤2.t为常数);若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示. 已知函数f(x)=ax3+
已知函数f(x)=ax3+