题目内容
已知定义在R上的偶函数f(x)满足f(1+x)=f(1-x),且x∈[0,1]时, ,则方程
,则方程 在区间[-3,3]上的根的个数为
在区间[-3,3]上的根的个数为
- A.5
- B.4
- C.3
- D.2
A
分析:由题意可得函数f(x)的图象关于x=1对称,函数y= 图象可看作y=
图象可看作y=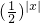 的图象向下平移1个单位得到,原问题等价于f(x)与y=
的图象向下平移1个单位得到,原问题等价于f(x)与y= 图象的交点的个数,作出它们的图象可得答案.
图象的交点的个数,作出它们的图象可得答案.
解答:由f(1+x)=f(1-x)可得函数f(x)的图象关于x=1对称,
方程 在区间[-3,3]根的个数等价于f(x)与y=
在区间[-3,3]根的个数等价于f(x)与y= 图象的交点的个数,
图象的交点的个数,
而函数y= 图象可看作y=
图象可看作y=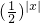 的图象向下平移1个单位得到,
的图象向下平移1个单位得到,
作出它们的图象如图:

可得两函数的图象有5个交点,
故选A
点评:本题考查根的存在性及根的个数的判断,数形结合是解决问题的关键,属中档题.
分析:由题意可得函数f(x)的图象关于x=1对称,函数y=
 图象可看作y=
图象可看作y=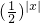 的图象向下平移1个单位得到,原问题等价于f(x)与y=
的图象向下平移1个单位得到,原问题等价于f(x)与y= 图象的交点的个数,作出它们的图象可得答案.
图象的交点的个数,作出它们的图象可得答案.解答:由f(1+x)=f(1-x)可得函数f(x)的图象关于x=1对称,
方程
 在区间[-3,3]根的个数等价于f(x)与y=
在区间[-3,3]根的个数等价于f(x)与y= 图象的交点的个数,
图象的交点的个数,而函数y=
 图象可看作y=
图象可看作y=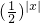 的图象向下平移1个单位得到,
的图象向下平移1个单位得到,作出它们的图象如图:

可得两函数的图象有5个交点,
故选A
点评:本题考查根的存在性及根的个数的判断,数形结合是解决问题的关键,属中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目