题目内容
已知二次函数f(x)=ax2+bx的图象过点(-4n,0),f′(x)是f(x)的导函数,且f′(0)=2n(n∈N*),(1)求a的值;
(2)若数列{an}满足
=f′(
),且a1=4,求数列{an}的通项公式;
(3)对于(2)中的数列{an},求证:a1+a2+a3+…+ak＜5(k=1,2,3,…).
答案：(1)解:由已知,可得f′(x)=2ax+b,1分
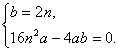∴解之,得a=.
(2)解:∵
=
+2n,∴
=2n.由
=2×1,
=2×2,
=2×3,…,
=2(n-1),累加得
=n2-n(n=2,3,…).
∴an=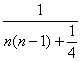
=
(n=2,3,…).当n=1时,
=4=a1,
∴an=
(n=1,2,3,…).
(3)证明:当k=1时,由已知a1=4＜5显然成立;
当k≥2时,ak=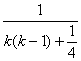
=
(k≥2),
则a1+a2+a3+…+ak＜4+［(1
)+(
-
)+…+(
)］=5
＜5.
综上,a1+a2+a3+…+ak＜5(k=1,2,3,…)成立.
练习册系列答案
相关题目