题目内容
解答题(本题共10分.请写出文字说明, 证明过程或演算步骤):
已知 是椭圆
是椭圆 上一点,
上一点, ,
, 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足
(Ⅰ)求椭圆方程;
(Ⅱ)设 、
、 是椭圆上任两点,且直线
是椭圆上任两点,且直线 、
、 的斜率分别为
的斜率分别为 、
、 ,若存在常数
,若存在常数 使
使 ,求直线
,求直线 的斜率.
的斜率.
【答案】
(I)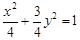 ;(II)
;(II)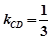 。
。
【解析】
试题分析:(I)根据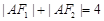 ,可知a=2,所以再把点A的坐标代入椭圆方程求出b的值,求出椭圆的方程.
,可知a=2,所以再把点A的坐标代入椭圆方程求出b的值,求出椭圆的方程.
(II)设直线AC的方程: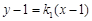 ,由
,由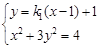 ,得:
,得:
点C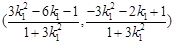 ,同理求出D的坐标,再利用斜率公式即可证明CD的斜率为定值.
,同理求出D的坐标,再利用斜率公式即可证明CD的斜率为定值.
(I) 所求椭圆方程
所求椭圆方程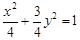 …………………3分;
…………………3分;
(II)设直线AC的方程: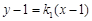 ,由
,由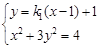 ,得:
,得:
点C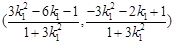 …………………………..5分;
…………………………..5分;
同理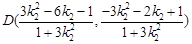 ………………………..6分;
………………………..6分;
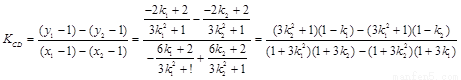
 ……………………8分;
……………………8分;
要使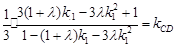 为常数,
为常数,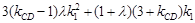 +(1-
+(1-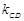 )=0,
)=0,
得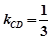 …………………………10分.
…………………………10分.
考点:椭圆的定义、标准方程,直线与椭圆的位置关系.
点评:椭圆上的点到两焦点的距离之和为定值,也就是常数2a,再根据其它条件建立关于b的方程,求出b即可得到椭圆的标准方程.
在证明CD的斜率为定值时,关键是求出点C,D的坐标,需要用直线方程与椭圆方程联立求解.

练习册系列答案
相关题目
 ,
,  的夹角为
的夹角为 , 且
, 且 ,
,  , 若
, 若 ,
,  , 求(1)
, 求(1) .
.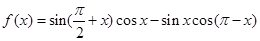 ,
, 的最小正周期;
的最小正周期;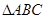 中,已知
中,已知 为锐角,
为锐角,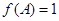 ,
,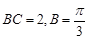 ,求
,求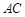 边的长.
边的长. ,
,  的夹角为
的夹角为 , 且
, 且 ,
,  , 若
, 若 ,
,  , 求(1)
, 求(1) .
.