题目内容
)设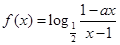 为奇函数,
为奇函数, 为常数.
为常数.
(1)求 的值;
的值;
(2)判断 在区间(1,+∞)内的单调性,并证明你的判断正确;
在区间(1,+∞)内的单调性,并证明你的判断正确;
(3)若对于区间 [3,4]上的每一个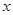 的值,不等式
的值,不等式 >
>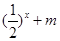 恒成立,求实数
恒成立,求实数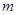 的取值范围.
的取值范围.
(1)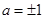 (2)在(1,+∞)上是增函数(3)
(2)在(1,+∞)上是增函数(3)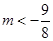
解析试题分析:解:(1)∵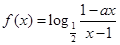 为奇函数,
为奇函数,
∴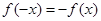 对于
对于 定义域中任意实数恒成立,
定义域中任意实数恒成立,
即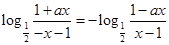 2分
2分
∴ ∴
∴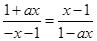 ∴
∴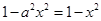
∴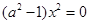 对于
对于 定义域中任意实数恒成立
定义域中任意实数恒成立
∵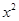 不恒为0,∴
不恒为0,∴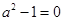 ∴
∴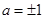 4分
4分
当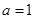 时
时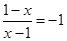 不符题意
不符题意
∴ 5分
5分
(2)由(1)得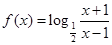
设1<x1<x2,则
f(x1)-f(x2)=log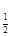
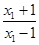 -log
-log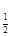
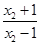 =log
=log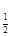
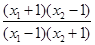
=log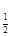
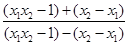 7分
7分
∵ 1<x1<x2,∴ x2-x1>0,
∴ (x1x2-1)+(x2-x1)>(x1x2-1)-(x2-x1)>0
即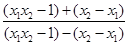 >1. 9分
>1. 9分
∴ f(x1)-f(x2)<0即f(x1)<f(x2),在(1,+∞)上是增函数 10分
(3)由(1),不等式 >
>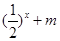 可化为
可化为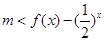 ,即
,即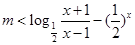
由题意得对于区间[3,4]上的每一个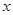 的值,
的值,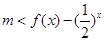 恒成立 2分
恒成立 2分
令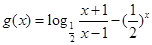 ,则
,则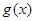 区间[3,4]上为增函数
区间[3,4]上为增函数
∵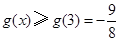 ∴
∴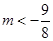 15分
15分
考点:函数性质的综合运用
点评:解决的关键是对于函数奇偶性和单调性的灵活运用,以及利用分离参数的思想求解函数的最值得到范围。属于中档题。

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
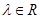 ,
,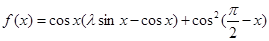 满足
满足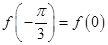 . (1) 求函数
. (1) 求函数 的单调递增区间;
的单调递增区间; 三内角
三内角 所对边分别为
所对边分别为 且
且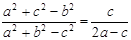 ,求
,求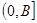 上的值域.
上的值域.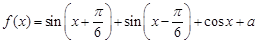 的最大值为1.
的最大值为1.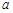 的值;(2)求使
的值;(2)求使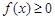 成立的x的取值集合.
成立的x的取值集合.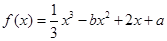 ,
,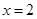 是
是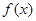 的一个极值点.
的一个极值点.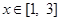 时,
时,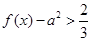 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. )的值;
)的值;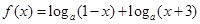 ,其中
,其中 ,记函数
,记函数 的定义域为D.
的定义域为D. ,求
,求 的值;
的值;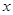 ,不等式
,不等式 <
<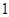 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.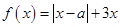 ,其中
,其中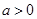 .
.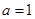 时,求不等式
时,求不等式 的解集;
的解集;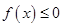 的解集为
的解集为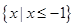 ,求
,求 的值.
的值.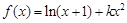 (
(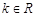 ).
).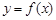 在
在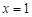 处取得极大值,求
处取得极大值,求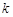 的值;
的值;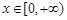 时,函数
时,函数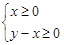 所表示的区域内,求
所表示的区域内,求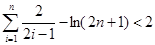 ,
,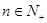 .
.