题目内容
已知对任意的实数m,直线x+y+m=0都不与曲线f(x)=x3-3ax(a∈R)相切,
(Ⅰ)求实数a的取值范围;
(Ⅱ)当x∈[-1,1]时,函数y=f(x)的图象上是否存在一点P,使得点P到x轴的距离不小于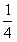 ,试证明你的结论。
,试证明你的结论。
(Ⅰ)求实数a的取值范围;
(Ⅱ)当x∈[-1,1]时,函数y=f(x)的图象上是否存在一点P,使得点P到x轴的距离不小于
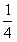 ,试证明你的结论。
,试证明你的结论。解:(Ⅰ)f′(x)=3x2-3a∈[-3a,+∞),
∵对任意m∈R,直线x+y+m=0都不与y=f(x)相切,
∴-1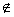 [-3a,+∞),-1<-3a,实数a的取值范围是
[-3a,+∞),-1<-3a,实数a的取值范围是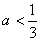 ;
;
(Ⅱ)存在,
证明:问题等价于当x∈[-1,1]时,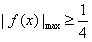 ,
,
设g(x)=|f(x)|,则g(x)在x∈[-1,1]上是偶函数,
故只要证明当x∈[0,1]时,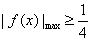 ,
,
①当a≤0时,f′(x)≥0,f(x)在[0,1]上单调递增,且f(0)=0,
g(x)=f(x),g(x)max=f(1)=1-3a>1>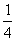 ;
;
②当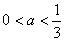 时,f′(x)=3x2-3a=
时,f′(x)=3x2-3a=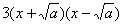 ,
,
列表:

f(x)在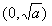 上递减,在
上递减,在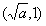 上递增,
上递增,
注意到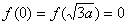 ,且
,且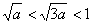 ,
,
∴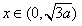 时,g(x)=-f(x),
时,g(x)=-f(x),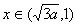 时,g(x)=f(x),
时,g(x)=f(x),
∴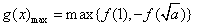 ,
,
由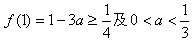 ,解得
,解得 ,此时
,此时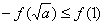 成立,
成立,
∴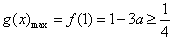 ,
,
由 ,解得
,解得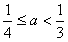 ,此时
,此时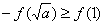 成立.
成立.
∴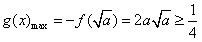 ,
,
∴在x∈[-1,1]上至少存在一个x0,使得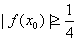 成立。
成立。
∵对任意m∈R,直线x+y+m=0都不与y=f(x)相切,
∴-1
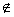 [-3a,+∞),-1<-3a,实数a的取值范围是
[-3a,+∞),-1<-3a,实数a的取值范围是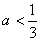 ;
;(Ⅱ)存在,
证明:问题等价于当x∈[-1,1]时,
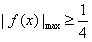 ,
,设g(x)=|f(x)|,则g(x)在x∈[-1,1]上是偶函数,
故只要证明当x∈[0,1]时,
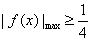 ,
,①当a≤0时,f′(x)≥0,f(x)在[0,1]上单调递增,且f(0)=0,
g(x)=f(x),g(x)max=f(1)=1-3a>1>
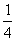 ;
;②当
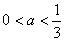 时,f′(x)=3x2-3a=
时,f′(x)=3x2-3a=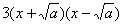 ,
,列表:

f(x)在
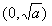 上递减,在
上递减,在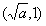 上递增,
上递增,注意到
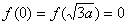 ,且
,且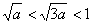 ,
,∴
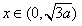 时,g(x)=-f(x),
时,g(x)=-f(x),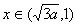 时,g(x)=f(x),
时,g(x)=f(x),∴
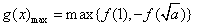 ,
,由
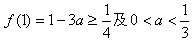 ,解得
,解得 ,此时
,此时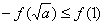 成立,
成立,∴
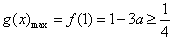 ,
,由
 ,解得
,解得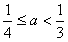 ,此时
,此时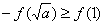 成立.
成立.∴
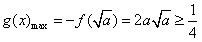 ,
,∴在x∈[-1,1]上至少存在一个x0,使得
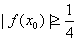 成立。
成立。
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
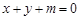 都不与曲线
都不与曲线 相切.
相切. 的取值范围;
的取值范围; 时,函数y=f(x)的图象上是否存在一点P,使得点P到x轴的距离不小于
时,函数y=f(x)的图象上是否存在一点P,使得点P到x轴的距离不小于 .试证明你的结论.
.试证明你的结论. .试证明你的结论.
.试证明你的结论.