题目内容
已知椭圆的焦点为F1(-1,0),F2(1,0),直线l:x-y+5=0,则
(1)经过直线l上一点P且长轴长最短的椭圆方程为________,(2)点P的坐标是________.
解:(1)设椭圆方程为  (a2>1),
(a2>1),
由 得(2a2-1)x2+10a2x+26a2-a4=0,
得(2a2-1)x2+10a2x+26a2-a4=0,
由题意,x此方程有解,∴△=(10a2)2-4(2a2-1)(26a2-a4)≥0,
∴a2≥13或a2≤1(舍),
∴a2min=13,此时椭圆方程是 .
.
(2)由(1)解方程25x2+10×13x+132=0,
得x=-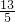 ,y=
,y= ,即点P的坐标为
,即点P的坐标为
故答案为: ;
; .
.
分析:(1)先设椭圆方程,然后与直线方程联立方程组,再根据该方程组有解即可求出a的最小值,则问题解决.
(2)根据(1)解方程25x2+10×13x+132=0,即可求出点P的横坐标,代入直线方程即可求得其纵坐标,从而求出点P的坐标.
点评:本题主要考查由代数方法解决直线与椭圆交点问题,考查运算能力,属中档题.
 (a2>1),
(a2>1),由
 得(2a2-1)x2+10a2x+26a2-a4=0,
得(2a2-1)x2+10a2x+26a2-a4=0,由题意,x此方程有解,∴△=(10a2)2-4(2a2-1)(26a2-a4)≥0,
∴a2≥13或a2≤1(舍),
∴a2min=13,此时椭圆方程是
 .
.(2)由(1)解方程25x2+10×13x+132=0,
得x=-
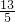 ,y=
,y= ,即点P的坐标为
,即点P的坐标为
故答案为:
 ;
; .
.分析:(1)先设椭圆方程,然后与直线方程联立方程组,再根据该方程组有解即可求出a的最小值,则问题解决.
(2)根据(1)解方程25x2+10×13x+132=0,即可求出点P的横坐标,代入直线方程即可求得其纵坐标,从而求出点P的坐标.
点评:本题主要考查由代数方法解决直线与椭圆交点问题,考查运算能力,属中档题.

练习册系列答案
相关题目