题目内容

已知
a1
=（1，0），
a2
=（1，-1），
a3
=（2，2），若
a1
+x
a2
+y
a3
=
0
，则x+y的值为
-
3
4
-
3
4
．
分析：由题意可得
1+x+2y=0
-x+2y=0
，解之可得x、y的值，进而可得答案．
解答：解：由题意可得
a1
+x
a2
+y
a3
=（1+x+2y，-x+2y）=（0，0）
故可得
1+x+2y=0
-x+2y=0
，解之可得
x=-
1
2
y=-
1
4
，
故x+y=-
1
2
-
1
4
=-
3
4
，
故答案为：-
3
4
点评：本题考查相等向量，由此建立方程组是解决问题的关键，属基础题．
练习册系列答案
相关题目
在平面直角坐标系中，已知A1（-3，0），A2（3，0），P（x，y），M(
x2-9
，0)，O为坐标原点，若实数λ使向量
A1P
，λ
OM
和
A2P
满足：λ2(
OM
)2=
A1P
•
A2P
，设点P的轨迹为W．
（Ⅰ）求W的方程，并判断W是怎样的曲线；
（Ⅱ）当λ=
3
3
时，过点A1且斜率为1的直线与W相交的另一个交点为B，能否在直线x=-9上找到一点C，恰使△A1BC为正三角形？请说明理由．
已知向量
a
=(1，0)，
b
=(x，1)，当x＞0时，定义函数f(x)=
a
•
b
|
a
|+|
b
|
．
（1）求函数y=f（x）的反函数y=f-1（x）；
（2）数列{an}满足：a1=a＞0，an+1=f（an），n∈N*，Sn为数列{an}的前n项和，则：
①当a=1时，证明：an＞
1
2n
；
②对任意θ∈[0，2π]，当2asinθ-2a+Sn≠0时，
证明：
2asinθ+2a-Sn
2asinθ-2a+Sn
≥
4a-Sn
Sn
或
2asinθ+2a-Sn
2asinθ-2a+Sn
≤
Sn
4a-Sn
．
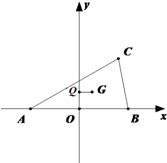设Q、G分别为△ABC的外心和重心，已知A（-1，0），B（1，0），QG∥AB．
（1）求点C的轨迹E．
（2）轨迹E与y轴两个交点分别为A1，A2（A1位于A2下方）．动点M、N均在轨迹E上，且满足A1M⊥A1N，试问直线A1N和A2M交点P是否恒在某条定直线l上？若是，试求出l的方程；若不是，请说明理由．
已知
a1
=（1，0），
a2
=（1，-1），
a3
=（2，2），若
a1
+x
a2
+y
a3
=
0
，则x+y的值为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网