题目内容
如图，点P在圆O直径AB的延长线上，且PB=OB=2，PC切圆O于C点，CD⊥AB于D点，则PC= ，CD= ．
【答案】分析：首先根据题中圆的切线条件再依据切割线定理求得PC2的值，再根据直角三角形中的边角关系即可求得PC和CD的长．
解答：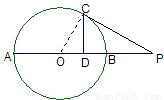
解：由切割线定理得PC2=PB•PA=12，
∴
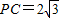；连接OC，则
，
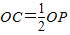∴∠P=30°，
∴
．
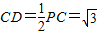故填：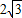
，
．
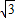点评：此题综合运用了切割线定理、切线的性质定理以及解直角三角形的知识，属于基础题．
解答：
解：由切割线定理得PC2=PB•PA=12，∴
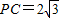；连接OC，则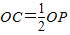，∴∠P=30°，
∴
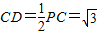．故填：
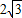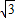，．点评：此题综合运用了切割线定理、切线的性质定理以及解直角三角形的知识，属于基础题．
练习册系列答案
相关题目
如图，点P在圆O直径AB的延长线上，且PB=OB=2，PC切圆O于C点，CD⊥AB于D点，则PC=
（考生注意：从下列三题中任选一题，多选的只按照第一题计分）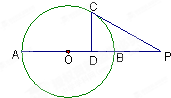
选做题（在（1）（2）中任选一题，若两题都做按第（1）题计分）
AB于点D，则CD=
。
AB于D点，则CD= 。