题目内容
设函数f(x)=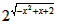 ,对于给定的正数K,定义函数
,对于给定的正数K,定义函数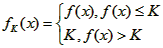 ,若对于函数
,若对于函数 定义域内的任意x,恒有
定义域内的任意x,恒有 ,则
,则
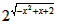 ,对于给定的正数K,定义函数
,对于给定的正数K,定义函数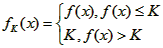 ,若对于函数
,若对于函数 定义域内的任意x,恒有
定义域内的任意x,恒有 ,则
,则[ ]
A.K的最大值为2
B.K的最小值为2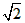
C.K的最大值为1
D.K的最小值为1

B.K的最小值为2
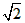
C.K的最大值为1
D.K的最小值为1
C

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
题目内容
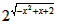 ,对于给定的正数K,定义函数
,对于给定的正数K,定义函数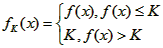 ,若对于函数
,若对于函数 定义域内的任意x,恒有
定义域内的任意x,恒有 ,则
,则

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案