题目内容
已知函数f(x)=2x3-2x2+x+ .
.(1)求证:f(x)在R上是增函数;
(2)设a1=0,an+1=
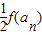 (n∈N+),b1=
(n∈N+),b1= ,bn+1=
,bn+1=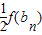 (n∈N+).
(n∈N+).①用数学归纳法证明:0<an<bn<
 (n>1,n∈N);
(n>1,n∈N);②证明:bn+1-an+1<
 (n∈N).
(n∈N).
【答案】分析:(1)通过函数的导数,判断导函数的正负,然后证明f(x)在R上是增函数;
(2)利用a1=0,an+1= (n∈N+),b1=
(n∈N+),b1= ,bn+1=
,bn+1=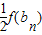 (n∈N+).
(n∈N+).
①直接利用数学归纳法证明的步骤证明:0<an<bn< (n>1,n∈N);
(n>1,n∈N);
②利用放缩法证明:bn+1-an+1<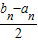 (n∈N).
(n∈N).
解答:证明:(1)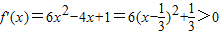 ,
,
∴f(x)在R上是增函数.…(4分)
(2)①用数学归纳法证明.1当n=2时,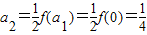 ,
,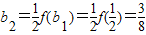 ,
,
∴ ,不等式成立.…(6分)
,不等式成立.…(6分)
2假设n=k(k>1,k∈N)时不等式成立,即 .
.
∵f(x)在R上是增函数,∴ ,
,
故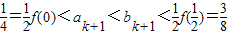 ,即
,即 ,
,
∴n=k+1时不等式也成立.
由1、2得不等式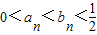 对一切n>1,n∈N都成立.…(10分)
对一切n>1,n∈N都成立.…(10分)
②由①知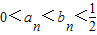 ,∴0<an+bn<1.
,∴0<an+bn<1.
∴
=
=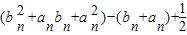 …(13分)
…(13分)
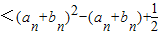
= .…(16分)
.…(16分)
点评:本题考查好的导数判断函数的单调性,数学归纳法证明不等式的方法,放缩法证明不等式的方法,考查分析问题解决问题的能力.
(2)利用a1=0,an+1=
 (n∈N+),b1=
(n∈N+),b1= ,bn+1=
,bn+1=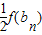 (n∈N+).
(n∈N+).①直接利用数学归纳法证明的步骤证明:0<an<bn<
 (n>1,n∈N);
(n>1,n∈N);②利用放缩法证明:bn+1-an+1<
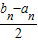 (n∈N).
(n∈N).解答:证明:(1)
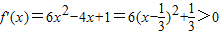 ,
,∴f(x)在R上是增函数.…(4分)
(2)①用数学归纳法证明.1当n=2时,
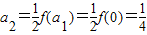 ,
,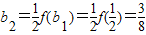 ,
,∴
 ,不等式成立.…(6分)
,不等式成立.…(6分)2假设n=k(k>1,k∈N)时不等式成立,即
 .
.∵f(x)在R上是增函数,∴
 ,
,故
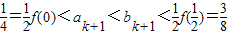 ,即
,即 ,
,∴n=k+1时不等式也成立.
由1、2得不等式
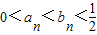 对一切n>1,n∈N都成立.…(10分)
对一切n>1,n∈N都成立.…(10分)②由①知
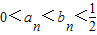 ,∴0<an+bn<1.
,∴0<an+bn<1.∴

=

=
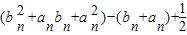 …(13分)
…(13分)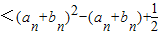
=
 .…(16分)
.…(16分)点评:本题考查好的导数判断函数的单调性,数学归纳法证明不等式的方法,放缩法证明不等式的方法,考查分析问题解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目